trygomometria Justa: Wyznacz zbiór wartości funkcji f(x)=1+2cosx−sin²x. Znajdź argumenty dla którego funkcja przyjmuje wartość najmniejszą. to co wykombinowałam: f(x)=sin²x+cos²x+2cosx−sin²x=cos²x+2cosx zastosuję zmienną t dla ułatwienia ⇒ t=cosx y=t²+2t ⇒t∊<−1;1> ⇒f w tym przedziale jest rosnąca

	−2
tw=		=−1 yw=−1 ⇒ZW=<−1;3>
	2

funkcja najmniejszą wartość przyjmuje dla t=−1 zatem cosx=−1 x=π+2kπ ; x=−π+2kπ jest ok? jeżeli są błędy, lub brak istotnych rzeczy, to proszę napisać

bezendu: cosx=−1 x=−π+2kπ k∊C

Justa: dlaczego tylko x=−π+2kπ ?

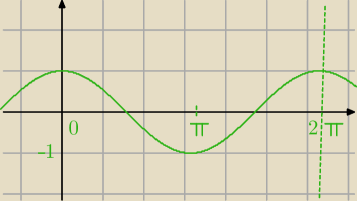Mila: Funkcja cos (x) ma okres zasadniczy 2π. W przedziale <0,2π> tylko raz przyjmuje wartość (−1). x=π+2kπ wystarczy podać . ( albo x=−π+2kπ)