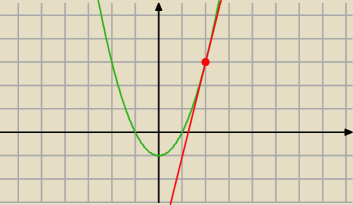
styczna do paraboli Lemon: Wyznacz równanie stycznej do paraboli f(x)=x²−1 w punkcie A=(2,3) Mam problem, bo jakieś herezje mi wychodzą. g(x) = ax+b A = (2,3) 3 = 2a+b b = 3−2a g(x) = ax+3−2a = a(x−2)+3 f(x)=g(x) x²−1=a(x−2)+3 x²−4=a(x−2) (x−2)(x+2)=a(x−2) /:(x−2)≠0 a=x+2 I co ja właściwie obliczyłem? Coś nie gra.

Tadeusz: ... i to jest cała matma ... znaleźć ścieżkę ... kroczyć po niej ... i w każdej chwili wiedzieć w którym punkcie jesteś !

Lemon: A ja właśnie zgubiłem swoją ścieżkę, ciemno jest. Potrzebuje latarki. Oświecisz mnie?

Tadeusz: 1 sposób Wyznaczyłeś g(x) ... z parametrem a Podstaw do równania paraboli. Styczna z krzywą mają jeden wspólny punkt ... czyli Δ=0 ... i tak policzysz a

Tadeusz: jeśli znasz pochodne ... to oczywiście jest prostszy sposób

Lemon: Ok, dziękuję, deltą poszło ładnie. Ale załóżmy, że doszedłem do tej postaci: (x−2)(x+2)=a(x−2) Da się dalej coś z tym zrobić?

Robaczek: Tadeuszu mógłbyś powiedzieć jak to policzyć z pochodnej?

Tadeusz: f'(x)=2x f'(2)=4 zatem masz napisać prostą przez A i mającą współczynnik kierunkowy 4 y−3=4(x−2) ⇒ y=4x−5

Robaczek: O to proste rzeczywiście. Dzięki!

ZKS: (x − 2)(x + 2) = a(x − 2) (x − 2)(x + 2 − a) = 0 Jedno rozwiązanie mamy x = 2 ale żeby prosta była styczna to musimy mieć tylko jedno rozwiązanie więc drugi nawias też musi mieć pierwiastek x = 2 x + 2 − a = 0 ⇒ 2 + 2 − a = 0 ⇒ a = 4.

Lemon: Ooo, super! Dzięki