Planimetria
bezendu:
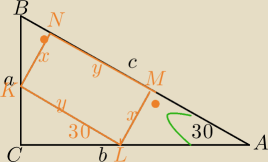
W trójkąt prostokątny o kącie ostrym ∘ 30 i przeciwprostokątnej długości 40 cm wpisujemy
prostokąty w ten sposób, że jeden bok każdego z tych prostokątów zawiera się w
przeciwprostokątnej trójkąta. Zbadaj który z tych prostokątów ma największe pole.
Proszę o wskazówkę
6 mar 18:40
Loki: Bok, które wpiszemy na przeciwprostokątną ma 2 wartość 20, a drugi bok √5. Następnie za
pomocą funkcji trygonometrycznych oblicz długości boków z jedną niewiadomą. Teraz dajesz
równanie kwadratowe i wierzchołek wyznacza Tobie tamta nie wiadoma, wstawiasz do poprzednich
równań i wszystko wychodzi
6 mar 18:54
bezendu: ok to robię
6 mar 19:00
Loki: Sorki za błędy, ale nie sprawdziłem sobie podglądu.Bok, który wpiszemy na przeciwprostokątną
ma wartość 20, a drugi bok 5√3. Następnie za pomocą funkcji trygonometrycznych oblicz
długości boków z jedną niewiadomą. Teraz dajesz równanie kwadratowe i wierzchołek wyznacza
Tobie tamta nie wiadoma, wstawiasz do poprzednich równań i wszystko wychodzi
6 mar 19:07
Mila:
6 mar 19:07
bezendu:
Loki nic z Twojego zapisu nie rozumiem, zrobię po swojemu.
Mila czy trójkąt CLK jest podobny do trójkąta ACB ?
6 mar 19:10
Ajtek:
Oczywiście.
Witam
Mila,
bezendu 
.
6 mar 19:19
bezendu:
Wyliczyłem
a=20
b=20√3
i teraz jak policzyć skalę podobieństwa ?
6 mar 19:21
Ajtek:
Jeżeli b=|CL| to w Δ ALM jest to |AM|
6 mar 19:24
bezendu: ?
6 mar 20:06
Mila:
Witajcie, [n{bezendu]] masz zaznaczony kąt 30 w obu Δprostokątnych ( dlaczego?) to są podobne,
bo są prostokątne i mają wszystkie kąty odpowiednio równe.
Masz tam Δ ekierkowe.
Uzależnij CL i LA od x i y
|CL|+|LA|=f(x,y)=20√3 stąd y
dalej sam
6 mar 20:15
bezendu:
Wiem, że w takich zadaniach muszę uzyskać funkcję kwadratową.
CL=20−√3b ?
6 mar 20:21
bezendu:
20−√3−b
6 mar 20:22
Mila:
Miałeś uzależnić od długości boków prostokąta x i y
|LA|=2x
P
▭=x*y
6 mar 20:28
bezendu:
Skąd CL=? i LA=?
6 mar 20:30
Mila:
w ΔKCL:
| | √3 | |
|CL|= |
| *y skoro nie widzisz "ekierki: |
| | 2 | |
W ΔLMA:
|LA|=2x skoro nie widzisz "ekierki:
6 mar 20:36
bezendu:
Teraz już chyba sobie poradzę, dziękuję.
6 mar 20:39
bezendu:
Po wielkich bólach wyszło poprawnie.
6 mar 21:34
Mila:
No to było zadanie z problemem, ale po wskazówce, to nie powinieneś mieć problemu.
Musisz uważniej patrzeć na te figurki.
6 mar 21:36
bezendu: Tak wiem, i myślę o tym. Robię codziennie po 20 parę zadań z planimetrii ale to jeszcze nie ten
poziom który chciałbym mieć, że zrobię każde zadanie z planimetrii i dowód bez wskazówki.
6 mar 21:37
Mila:
No to następne pisz .
6 mar 21:48
bezendu:

Na rysunku okręgi o środkach B i C są styczne zewnętrznie i jednocześnie są styczne
wewnętrznie do okręgu o środku w punkcie A . Wykaż, że jeśli |BC | = |AC | , to długość
odcinka AB jest równa długości średnicy okręgu o środku w punkcie C .
Wskazówka
6 mar 21:55
Mila:
Połącz środki tych trzech okręgów, zrób sobie dobry rysunek za pomocą cyrkla.
6 mar 22:12
bezendu:
Zrobiłem ten rysunek i mam
długość odcinak BC=rb+rc
długość odcinka AC=rb+rc
długość odcinka AB ? ra−rb ?
6 mar 22:15
Mila:
Bardzo dobrze.
Tak i dalej na inny sposób |AC|=ra−rc
ra−rc=rb+rc⇔
ra−rb=2rc⇔AB=2rc
6 mar 22:29
bezendu:
I to jest koniec dowodu. Niby banał.
6 mar 22:33
bezendu:
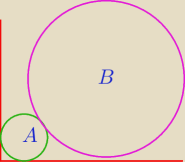
Dwa okręgi o środkach A i B są styczne zewnętrznie i każdy z nich jest jednocześnie styczny
do ramion tego samego kąta prostego. Udowodnij, że stosunek promienia większego z tych okręgów
do promienia mniejszego jest równy 3 + 2√ 2
6 mar 22:35
Mila:
Środki okręgów leżą na dwusiecznej kąta prostego.
Połącz środki z ramoinami, powstaną kwadraty.
6 mar 22:47
bezendu:
Nie mogę tutaj narysować tak dwusiecznej aby przechodziła przez środki okręgów.
6 mar 22:57
Mila:
Nie szkodzi narysuj sobie na kartce.
Podpowiedź:
Oblicz przekątne kwadratów.
6 mar 23:05
Mila:
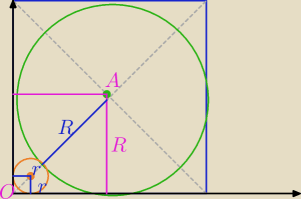
6 mar 23:10
bezendu:
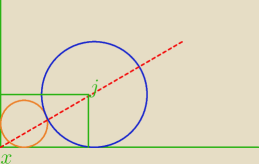
2 pytania.
1. Skąd wiadomo, że środki leżą na dwusiecznej
2. Jak policzyć te przekątne jak mam promień dużego, średnice małego i jeszcze ten x ?
Wiem, że rysunek źle ale chodziło mi tylko o ten x
6 mar 23:11
Mila:
środek okręgu wpisanego w kąt leży na dwusiecznej kąta, bo jego odległość jest jednakowa od
ramion kąta.
Patrz na mój rysunek
|OA|=R√2 − przekątna większego kwadratu.
r√2− − przekątna mniejszego kwadratu.
|OA| na drugi sposób?
R√2=...
6 mar 23:17
bezendu:
Jak będę wiedział skąd to r√2 to wiem wszystko.
6 mar 23:22
Mila:
To są kwadraty o bokach R i r.
Znasz przecież wzór na przekątną kwadratu.
6 mar 23:23
bezendu:
Tak znam, ale nie wiem nadal skąd się to wzięło.
6 mar 23:26
Mila:
Punkt A leży na prostej y=x zatem
ma współrzędne (R,R)
6 mar 23:30
bezendu: No tak.
6 mar 23:31
Antek: No i co . dalej twierdzisz ze mozna troche liznac teorii i juz sie nauczysz zadania rozwiazywac
?
Nie da sie tak
6 mar 23:36
bezendu:
Znam teorię a Twój komentarz niestety nie wnosi nic do rozwiązania

6 mar 23:43
Mila:
No to co z tym zadaniem?
6 mar 23:50
bezendu:
Już wiem. Dziękuję.
6 mar 23:50
Mila:
|OA|=R
√2=R+r+r
√2
R
√2−R=r+r
√2
R(
√2−1)=r(1+
√2) /*(
√2+1)
R*(2−1)=r*(
√2+1)
2
Dobranoc

6 mar 23:54
bezendu:
To już wiedziałem tylko najwięcej problemu sprawiło mi skąd r√2. Ja jeszcze muszę liczyć
zadania.
Dobranoc.
6 mar 23:56
7 mar 00:02
bezendu:
Dziękuję, nie będę już kupował żadnych książek obecnie mam 10 i to mi wystarczy.

7 mar 00:03
bezendu:
wracając do zadania 6 marzec 21:55
to moim sposobem nie wychodzi to zadanie
|BC|=|AC|
|BC|=rc+rb
|AC|=rc+rb
|AB|=ra−rb
|AB|=2rc
8 mar 20:30
bezendu: ?
8 mar 20:44
Mila:
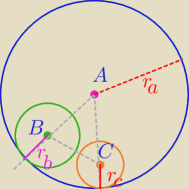
|AC|=|BC| z treści
|AB|=r
a−
rb z rysunku.
|AC|=r
a−
rc=r
b+r
c⇔r
a−r
b=2r
c
8 mar 20:55
bezendu:
Ja wiem, że z przyrównania AC=BC to wychodzi ale czemu nie chcę wyjść z tego ?
|BC|=|AC|
|BC|=rc+rb
|AC|=rc+rb
|AB|=ra−rb
Z treści mam że |BC|=|AC|
ra−rb=2rc ?
ra−rb−2rc=0
ra−rc−rb−rc=0
I tutaj nie wychodzi
8 mar 21:01
bezendu: ?
8 mar 21:22
Mila:
Dlaczego wychodzisz od tezy i kombinujesz?
8 mar 21:23
bezendu:
Tak mam podane w zadaniu to chcę do tego dojść.
8 mar 21:24
Mila:
Co ma Ci wyjść założenie?
To masz
ra−rc=rb+rc i to było złożone, Tak jednak nie należy rozwiązywac.
8 mar 21:35
bezendu:
Dziękuję, bo tym nie chciało wyjść i zastanawiałem się gdzie robię błąd.
8 mar 21:36
Mila:
Rozwiązałeś maturkę R z drugiej? Naprawdę warto.
8 mar 21:38
bezendu:
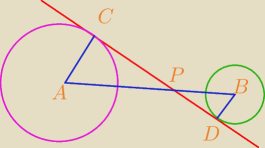
Do dwóch okręgów o promieniach długości 3cm i 10cm poprowadzono wspólną styczną tak, że okręgi
znajdują się po różnych stronach tej stycznej. Odległość między środkami okręgów wynosi 39 cm.
Oblicz długość odcinka między punktami styczności.
z podobienstwa
8 mar 21:40
bezendu:
Rozwiązałem i rozwiązałem również z zadania.info tylko tego dowodu z podstawy ruszyć nie mogę.
8 mar 21:41
Mila:
No, dobrze, licz dalej.
8 mar 21:48
bezendu:
10|PD|=117−3|PD|
13|PD|=117
|PD|=9
CP=30
Można jakoś inaczej policzyć ?
8 mar 21:50
Mila:
Po co szukasz problemów, jest dobrze, dokończ z tw. Pitagorasa.
8 mar 21:53
bezendu:
Nie szukam problemów, po prostu chcę znać wszystkie metody rozwiązania. Kiedyś radziłaś mi żeby
rozwiązywać na kilka sposobów i wybrać najlepszy, dlatego pytam.
8 mar 21:55
Mila: Zaraz podam.
8 mar 21:58
Mila:
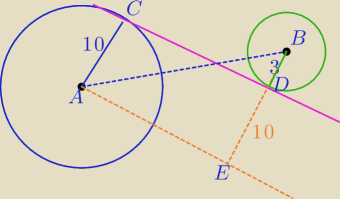
AE||CD
|CD|=|AE|
AB
2=AE
2+BE
2
39
2=AE
2+13
2
8 mar 22:05
bezendu:
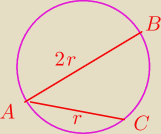
W okręgu o promieniu długości r kreślimy średnicę AB oraz taką cięciwę AC , że |AC | = r .
Jaką częścią okręgu jest łuk CAB ?
8 mar 22:15
Mila:
Oblicz miarę kąta CAB.
8 mar 22:43
zawodus: co to za łuk?
8 mar 22:43
bezendu:

8 mar 22:45
bezendu:
Hmm?
8 mar 23:09
5-latek: no dobrze zaczales kombinowac
8 mar 23:14
Mila:
α=60 kąta wpisany CAB
β=120 kąt środkowy COB
360−120=240
Powtórz pole wycinka, długość łuku.
8 mar 23:14
bezendu:
Dziękuję już wszystko ładnie wychodzi

8 mar 23:16

 .
.
 Na rysunku okręgi o środkach B i C są styczne zewnętrznie i jednocześnie są styczne
wewnętrznie do okręgu o środku w punkcie A . Wykaż, że jeśli |BC | = |AC | , to długość
odcinka AB jest równa długości średnicy okręgu o środku w punkcie C .
Wskazówka
Na rysunku okręgi o środkach B i C są styczne zewnętrznie i jednocześnie są styczne
wewnętrznie do okręgu o środku w punkcie A . Wykaż, że jeśli |BC | = |AC | , to długość
odcinka AB jest równa długości średnicy okręgu o środku w punkcie C .
Wskazówka
 Dwa okręgi o środkach A i B są styczne zewnętrznie i każdy z nich jest jednocześnie styczny
do ramion tego samego kąta prostego. Udowodnij, że stosunek promienia większego z tych okręgów
do promienia mniejszego jest równy 3 + 2√ 2
Dwa okręgi o środkach A i B są styczne zewnętrznie i każdy z nich jest jednocześnie styczny
do ramion tego samego kąta prostego. Udowodnij, że stosunek promienia większego z tych okręgów
do promienia mniejszego jest równy 3 + 2√ 2

 2 pytania.
1. Skąd wiadomo, że środki leżą na dwusiecznej
2. Jak policzyć te przekątne jak mam promień dużego, średnice małego i jeszcze ten x ?
Wiem, że rysunek źle ale chodziło mi tylko o ten x
2 pytania.
1. Skąd wiadomo, że środki leżą na dwusiecznej
2. Jak policzyć te przekątne jak mam promień dużego, średnice małego i jeszcze ten x ?
Wiem, że rysunek źle ale chodziło mi tylko o ten x



 |AC|=|BC| z treści
|AB|=ra−rb z rysunku.
|AC|=ra−rc=rb+rc⇔ra−rb=2rc
|AC|=|BC| z treści
|AB|=ra−rb z rysunku.
|AC|=ra−rc=rb+rc⇔ra−rb=2rc
 Do dwóch okręgów o promieniach długości 3cm i 10cm poprowadzono wspólną styczną tak, że okręgi
znajdują się po różnych stronach tej stycznej. Odległość między środkami okręgów wynosi 39 cm.
Oblicz długość odcinka między punktami styczności.
z podobienstwa
Do dwóch okręgów o promieniach długości 3cm i 10cm poprowadzono wspólną styczną tak, że okręgi
znajdują się po różnych stronach tej stycznej. Odległość między środkami okręgów wynosi 39 cm.
Oblicz długość odcinka między punktami styczności.
z podobienstwa
 AE||CD
|CD|=|AE|
AB2=AE2+BE2
392=AE2+132
AE||CD
|CD|=|AE|
AB2=AE2+BE2
392=AE2+132
 W okręgu o promieniu długości r kreślimy średnicę AB oraz taką cięciwę AC , że |AC | = r .
Jaką częścią okręgu jest łuk CAB ?
W okręgu o promieniu długości r kreślimy średnicę AB oraz taką cięciwę AC , że |AC | = r .
Jaką częścią okręgu jest łuk CAB ?

