ze zbioru Matejko: ze zbioru Z={ −1,0,1,2,3} losujemy kolejno bez zwracania współczynniki a b c funkcji y=ax²+bx+c Oblicz prawdopodobieństwo zdarzenia: B)−Otrzymana funkcja jest malejąca w przedziale (−∞;−1) i rosnąca w przedziale (−1;+∞) C)−prosta o równaniu x=0 jest osią symetrii otrzymanego wykresu funkcji proszę o pomoc

Matejko:

Mila: Jakieś przemyślenia masz? Jak zachowuje się funkcja kwadratowa jeśli chodzi o monotoniczność?

anonim: B − równanie musi mieć jedno miejsce zerowe na −1 oraz a≠−1 i a≠0

bezendu:

	5 3
Ω=

a=1 b=2

	−b
xw=
	2a

anonim: czyli (x+1)² b=2 c = 1 i z tego zostaje, że a musi byc równe 3.

bezendu: @anonim widać, że nie znasz definicji funkcji kwadratowej

	−2
xw=		≠−1
	2*3

i w tym zadaniu c akurat nie jest istotne bo może być dowolne.

Matejko: wiem że wszystkich jest 5*4 czyli 20 a>0 i −4ac=0

bezendu: Niby czemu 5*4 ? Przecież losujemy a,b,c więc już masz źle.

Matejko: 5*4*3=60 ===>Ω

Matejko: mi wyszły punkty 1 −1 0 1 2 0 1 3 0 2 −1 0 2 1 0 2 3 0 3 −1 0 3 1 0 3 2 0 ale odpowiedź to ¹₂₀ a mi wyszło ³₂₀

bezendu: a− musi być równe 1 b−musi być równe 2 c−dowolne

	?
P(A)=
	Ω

Matejko: mam już zrobiłem tak że (x+1)² jest rozwiązaniem ale przez nawias możemy dać 1 2 lub 3 i wyszło 0,05 a jak B zrobić?

bezendu: To jest proste zadania, pisałem ale Ty nie słuchasz wskazówek, więc nie wiem po co piszę ? A−musi być 1 B−musi być 2 C−dowolne

	1*1*3		1
P(A)=		=
	6*5*4		20

Matejko: wiem wiem bezendu anonim mnie zmylił proszę o pomoc w B

bezendu: A co rozwiązałem jak nie B ?

bezendu: C) a−dowolne b=0 c−dowolne

Matejko: a dlaczego b 0?

bezendu: Ty też nie znasz definicji funkcji kwadratowej ? oś symetrii to x_w

0
	=0
coś

Matejko: znam wiedziałem na na osi Oy musi leżen czyli punkt (0;cos) ale próbowałem zrobić tak żeby w mianowniku było zero no ale przecież nie można dzielić przez zero dzięki za pomoc w zadaniach jesteście świetni może zdam ładnie maturę z matematyki

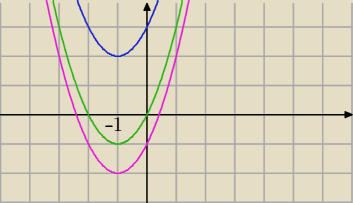
Mila: a) |Ω|=5*4*3 A−Otrzymana funkcja jest malejąca w przedziale (−∞;−1) i rosnąca w przedziale (−1;+∞) Zmiana monotoniczności zachodzi dla x_w

	−b
xw=−1⇔		=−1
	2a

b=2a i a>0 c może być dowolne Zdarzenia sprzyjające: (1,2,0) (1,2,3) (1,2,−1)

	3		1
P(A)=		=
	5*4*3		20

b) x_w=0 jest osią symetrii ⇔b=0 Zdarzenia sprzyjające (−1,0,1) (−1,0,2) (−1,0,3) (1,0,−1) (1,0,2) (1,0,3) ...... dokończ , |B|=4*3

bezendu: Czyli Mila potwierdziła moje rozwiązania Tylko moje wersja skrócona.