planimetria Anka: W trójkącie ABC kąt przy wierzchołku B jest ostry, długość promienia okręgu opisanego na tym trójkącie jest równa 5 oraz AC =6, AB =10. Na boku BC wybrano taki punkt K, że BK =2. Oblicz długość odcinka AK.

Anka: ?

Antek: a rysunek zrobiony?

Anka: tak na kartce, wydaje mi się iż to jest tr prostokątny AB = 2R, dobrze myślę?

Eta: α −− kąt ostry R=6

	6		3
z tw. sinusów trójkącie ABC		=2R ⇒ sinα=
	sinα		5

to cosα= +√1−sin²α= ..... i z tw. kosinusów w trójkącie ABK x²= .........

muflon: z jakiej paki R =6

Antek: Nic nie szkodzi. Jak dziewczyna mysli to zauwazy blad i wstawi za R=5

Eta: tzn. źle wpisałam ( literówka)

	6		3
R=5 ⇒		= 2R=10 ⇒ sinα=		i wszystko gra
	sinα		5

muflon nie irytuj się ( bo ci rogi muflona odpadną

muflon: hahahha , a wtedy można stwierdzić że to jest prostokątny? o czym anka wspominała? i z pitagorasa obliczyć bok a potem odcinek?

muflon: ?

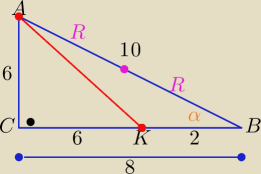
Eta: 2R=10 |AK|=6√2

muflon: Dzięki