analityczna Radek: W prostej o równaniu 2x+y+6=0 zawiera się bok kwadratu opisanego na okręgu o równaniu x²+y²−2y−4=0 wyznacz wsp wierzchołków (0,−4) (0,6) (−4,4) (4,−2) ?

bezendu: Chyba nie takie te punkty.

Mila: Rozwiąż Bezendu.

Aerodynamiczny: układ równań 2 stopnia a pozostałe 2 za pomocą wektorów najszybciej. A jak to zrobiłeś? Jak znajdę kartkę to sprawdzę

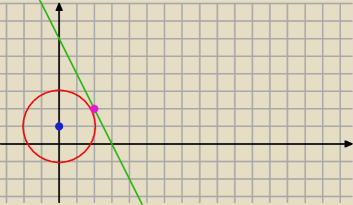
bezendu: 2x+y−6=0⇒y=−2x+6 Punkt styczności z okręgiem x²+(−2x+6)²−2(−2x+6)=5 5x²−20x+20=0 x²−4x+4=0 (x−2)²=0 A=(2,2) Długość promienia to połowa boku (x−2)²+(−2x+6−2)²=5 I z tego wychodzi równanie kwadratowe dające już inne punkty jak Twoje

Tadeusz: ... zacznij od sprawdzenia treści zadania

bezendu: Prosta równoległa do prostej y=−2x+6 ma równanie postaci y=−2x−4 Wyznaczam wierzchołki na prostej y=−2x−4 (punkt styczności B=(−2,0) (x+2)²+(−2x−4)²=5 x²+4x+4+4x²+16x+16−5=0 5x²+20x+15=0 x²+4x+3=0 Δ=4 √Δ=2

	−4−2
x1=		=−3
	2

	−4+2
x2=		=−2
	2

y₁=2 y₂=0 Więc albo ja się mylę albo Ty.

Tadeusz: ... TYLE, ŻE W TREŚCI jest inne równanie prostej Patrz na znaki

bezendu: Ja takie zadanie widziałem w zielonym Aksjomacie i znaki były tak jak ja podałem. Bo przepisałem z mojego arkusza. Ale niech wypowie się autor.

Radek: Przepraszam prosta zawierająca bok ma równanie 2x+y−6=0

Tadeusz: napisałem mu to w poście z 18:11 .... ale on wrzucił zadanko i ma to w poważaniu ...

bezendu: Tadeusz czyli moje rozwiązanie ok ?

Radek: Przeprosiłem już i nie mam nic w poważaniu !

Tadeusz: ... przepraszam ....ale nie sprawdzałem W zgaduj−zgadulach nie biorę udziału −

bezendu: a ktoś tu mówi o zgaduj zgadula ? Napisałem przecież jak wyliczyłem ?

bezendu: Potwierdzi ktoś mój wynik ?

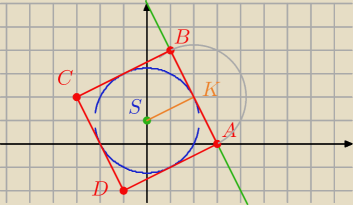
Mila: W prostej o równaniu 2x+y−6=0 zawiera się bok kwadratu opisanego na okręgu o równaniu x²+y²−2y−4=0 wyznacz wsp. wierzchołków . 2x+y−6=0⇔y=−2x+6 Ronanie okręgu: x²+(y−1)²−1−4=0 x²+(y−1)²=(√5)² postać kanoniczna. r=√5 Punkt styczności: x²+(−2x+5)²=5 x=2, y=2 K(2,2) środek boku kwadratu a=2r=2√5 długość boku kwadratu. Kreślę okrąg o środku K(2,2) i R=√5 (x−2)²+(y−2)²=5 i y=−2x+6 Znajduję punkty przecięcia (x−2)²+(−2x+6−2)²=5 (x−2)²+(−2x+4)²=5⇔ x=1 lub x=3 y=4 lub y=0 A=(3,0) B=(1,4) C(x_c,y_c) wsp. obliczę korzystając z symetrii wzdględem punktu S. S jest środkiem AC i BD S=(0,1)

	xc+3		yc+0
0=		, 1=
	2		2

x_c+3=0 i y_c=2 x_c=−3, y_c=2 C=(−3,2) D(x_d,y_d)

	xd+1		yd+4
0=		, 1=
	2		2

x_d=−1, y_d=−2 D(−1,−2) Odp. A=(3,0) B=(1,4) C=(−3,2) D(−1,−2)

Mila: Taka jest odp.?

bezendu: Ja liczyłem tak jak Ty Mila tylko tam drobny błąd w znakach

Radek: Taka jest odp (0,−4) (0,6) (−4,4) (4,−2)

Mila: Radek zobacz czy moja treść się zgadza z tą co w książce.

Radek: Tak zgadza się arkusz 10 zadanie 6 http://www.aksjomat.torun.pl/_var/gfx/9d277de9e387c2ac67c67b1e95a1c665.jpg

Mila: To ja zaraz sprawdzę, gdzie się pomyliłam, ale teraz mam przerwę na kolację. Bezendu, sprawdx w Twojej książce zgodność mojej treści i odpowiedź.

bezendu: Mila masz dobrze, w tej książce jest pełną błędów. Zresztą mi wyszły takie same wyniki

Radek: Dziękuję.