wielomiany dmi: nie rozumiem jak rozwiązać zadania z wart. bezwzględną przy wielomianach, mógłby ktoś mi wyjanić jak mam postepować na dwóch−trzech przykładach? a) 5|x|+2|x|³≥0 b)|x+1|³−3|x+1|²≥0 c)|x³−4x|>x³−4x

pigor: ..., np. a) 5|x|+2|x|³ ≥0 ⇔ |x| (2|x|²+5) ≥0 ⇔ x∊R ,

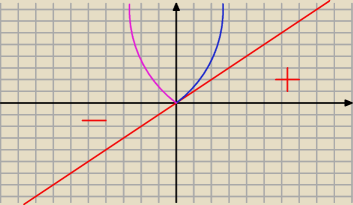
Domel: Moja metoda (może nie najkrótsza ale chyba pewna) wygląda tak: 1. Wyznaczam miejsca zerowe wszystkich funkcji ograniczonych |...| 2. Otrzymuję przedziały rozpatrywania od −oo do 1−go punktu zerowego, między punktami zerowymi i od ostatniego punktu zerowego do +oo 3. W poszczególnych przedziałach określam znaki funkcji 4. Rozwiązuję działanie w poszczególnych przedziałach Dla przykładu twoje zadanie a) − tam w |...| jest tylko jeden typ funkcji y = x 1. Miejsce zerowe − x = 0 2. Mam przedziały (−oo; 0) i (0; +oo) 3a. W przedziale (−oo; 0) → |x| = −x więc 5|x| + 2|x|³ = 5(−x) + 2(−x)³ = −5x − 2x³ −5x − 2x³ ≥ 0 −x(5 + 2x²) ≥ 0 x(5 + 2x²) ≤ 0 x < 0 ∨ 5 + 2x² > 0 Ponieważ funkcja 5 + 2x² jest zawsze dodatnia (współczynnik "a" równania kwadratowego > 0 i brak miejsca zerowego bo Δ < 0) a x∊(−oo; 0) to 5|x| + 2|x|³ ≥ 0 w całym przedziale 3b. W przedziale <0; +oo) → |x| = x więc 5|x| + 2|x|³ = 5x + 2x³ 5x + 2x³ ≥ 0 x(5 + 2x²) ≥ 0 x ≥ 0 ∨ 5 + 2x² > 0 Ponieważ funkcja 5 + 2x² jest zawsze dodatnia (opis powyżej) a x∊<0; +oo) to 5|x| + 2|x|³ ≥ 0 w całym przedziale Więc x∊R

pigor: ..., b) |x+1|³−3|x+1|² ≥ 0 ⇔ |x+1|² (|x+1| −3) ≥0 ⇔ |x+1| −3 ≥0 ⇔ |x+1| ≥3 ⇔ ⇔ x+1≤ −3 v x+1 ≥3 ⇔ x ≤ −4 v x ≥ 2 ⇔ x∊(−∞;−4] U [2;+∞). ...

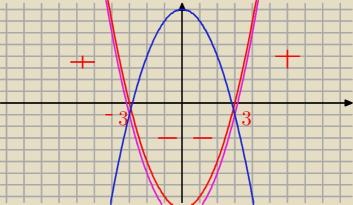
Domel: Dam ci inny przykład a ty pokombinujesz ze swoimi: |x² − 9| < 1 Mamy tu funkcję w |...| f(x) = x² − 9 − miejsca zerowe x = ±3 − parabola czerwona 1. dla x∊(−oo; −3> ∨ <3; +oo) => |x² − 9| = x² − 9 x² − 9 < 1 x² − 10 < 0 x = ±√10 Biorąc pod uwagę przedział w pkt 1. x∊(−√10; −3> ∨ <3; √10) 2. dla x∊(−3; 3) => |x² − 9| = −x² + 9 −x² + 9 < 1 −x² + 8 < 0 x = ±√8 Biorąc pod uwagę przedział w pkt 2. x∊(−3; −√8) ∨ (√8; 3) Łącząc przedziały końcowe z pkt 1. i 2.: x∊(−√10; −√8) ∨ (√8; √10)

pigor: .., i jeszcze przykład c) |x³−4x| >x³−4x ⇔ x³−4x< 0 ⇔ x(x²−4)< 0 ⇔ x(x−2)(x+2)< 0 ⇔ ⇔ x<−2 v 0< x< 2 ⇔ x∊(−∞;−2) U (0;2) . ...

pigor: ..., no, a zobaczmy jeszcze przykład : |x²−9|<1 ⇔ −1< x²−9< 1 /+9 ⇔ 8< x²< 10 ⇔ √8< |x|< √10 ⇔ ⇔ |x| >√8 i |x|< √10 ⇔ (x<−√8 v x >√8) i −√10< x< √10 ⇔ ⇔ −√10< x< −√8 v √8< x< √10 ⇔ x∊(−√10;−2√2) U (2√2; √10) .