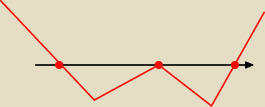
Kilka pytan odnośnie funkcji wielomianowych FHA: 1) Wykres zawsze od prawej do lewej? Tak 2) Jeżeli wspólczynniki przy najwyzszej potędzie + to od góry, jeżeli minus to od dolu? Tak 3) Co robimy gdy mamy pierwiastek dwukrotny i jak wygląda wykres? np. (x−2)² x − 2 = 0 x = 2, −> pier. 2− krotny Powiedzmy że mamy jeszcze pierwiastek: −1 , 5 a a₄ −> + wykres:

Ajtek: Przy pierwiastku parzystego stopnia nie przechodzisz, przez oś, odbijasz się od niej.

FHA: Czyli to co zaprezentowalem wyżej jest ok?

ZKS: Jeżeli a₄ oznacza że współczynnik przy najwyższej potędze jest dodatni to tak.

FHA: Tak, dlatego idzie od góry. Dalem dla przykładu

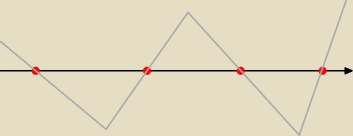
FHA: Teraz kolejny przykład dla utralenia nieobecnośći na tej lekcji: a₄ − wspólczynniki przy najwyższej potędze ( dodatni ) Pierwiastki: 5, 3 , 1( stopnia ³ np: (x−1)³ ⇒ x = 1, stop. 3), −2 powiedzmy dla: ≥ 0 wykres: x ∊ ( − ∞, −2 > u <1,3> u <5,+∞) dobrze?

ZKS: Dziwnie zapisujesz to że współczynnik przy najwyższej potędze jest dodatni a₄? Jedynie się mogłem domyślić co oznacza te a₄.

ZKS: Ten post było do wcześniejszego rysunku tutaj wyjaśniasz co oznacza te a₄.

ZKS: Wynik .

FHA: Dziękuje Ajtek i ZKS za potwierdzenie i drobną pomoc

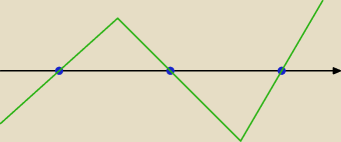
FHA: Mam takie zadanko: 3x² ≤ |x³ − 4x| 1. x³ −4x ≥ 0 x(x² − 4) ≥ 0 x = 0 x= −2, 2 Wykres: x ∊ < −2, 0> u <2, +∞ ) 3x² ≤ x³ − 4x 3x² −x³ − 4x ≤ 0 x(3x − x² + 4 ) ≤ 0 x(−x² + 3x + 4) ≤ 0 √Δ = 5 x = 0 x₁ = 4 x₂ = −1 Wykres:

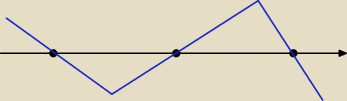
FHA: x ∊ < −1, 0 > u < 4+ ∞ ) wiec zgodne z zalozeniem 2. Czyli mamy tez zalozenie < −2,0> u <2+∞) i sprawdzamy dla wartosci pod modulem z przeciwnymi znakami? dobrze jest?

FHA: zaraz dokończe

FHA: Czy do tej pory jest git? Nie mam zamiaru mazac

Ajtek: Narysuj te dwa wykresy na jednej ośce tutaj. Oznacz zamiast kropek konkretne liczby. Na razie wygląda to okej. Ale chcę to zobaczyć

ZKS: Po co tak? Dla każdego x ∊ R wyrażenie 3x² jest nieujemne więc moduł możemy rozpatrywać tak |x| ≥ a gdzie a ≥ 0 x ≥ a ∨ x ≤ −a. Wtedy nie trzeba rozwiązywać nierówności x³ − 4x ≥ 0 oraz x³ − 4x < 0. 3x² ≤ |x³ − 4x| x³ − 4x ≥ 3x² ∨ x³ − 4x ≤ −3x² x³ − 3x² − 4x ≥ 0 ∨ x³ + 3x² − 4x ≤ 0

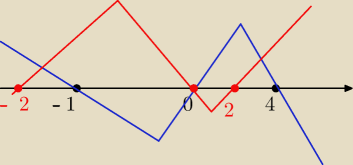
FHA: proszę

FHA: ZKS, tak zacząlem Zaraz dokończe

FHA: już jestem, już to kończe

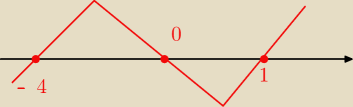
FHA: 2. x³ − 4x <0 ⇒ x ∊ < −2,0> u < 2,+ ) 3x² ≤ −x³ + 4x 3x² + x³ − 4x ≤ 0 x(3x + x² − 4 ) ≤ 0 x(x² + 3x −4 ) ≤ 0 Δ = 25 x₁ = −3 +5 / 2 = 1 x₂ = −3 − 5 /2 = −4 x = 0 wykres: x ∊ ( − ∞m −4 > u <0 , 1 > ⇒ sprzeczne z zalozeniem na koniec: hmm?

FHA: Gdzieś się rypnąlem, końcowy wynik x ∊ ( − ∞, −4 ) u <−1,1> u < 4,+ ∞ )

ZKS: x³ − 4x < 0 ⇒ x ∊ [−2 ; 0] ; [2 ; ∞) czy aby na pewno?

FHA: x ∊ ( − ∞,−2 ) u ( 0,2 ), gapa ze mnie

FHA: Teraz się wszystko zgadza

FHA: dziękuje i dobrej nocy