pochodna pomocy: jak obliczyc pochodna y={x} ? (czesc calkowita)

Godzio: Tak się oznacza część ułamkową (część całkowita − [x] )

f(x + h) − f(x)		[x + h] − [x]
	=
h		h

Problem jest tylko w punktach nieciągłości x = n ∊ N

[n + h] − [n]		n + [h] − n		[h]
	=		=
h		h		h

h → 0⁺ granica jest równa 0

	−1
h → 0− granica jest równa		= ∞
	0−

Zatem pochodna w punktach całkowitych nie istnieje, po za tym pochodna jest równa 0.

pomocy: no wlasnie pomylilo mi sie chodzilo mi o czesc ulamkowa

Godzio: Eh ! Próbuj analogicznie ( {x} = x − [x] − powinno z tego pójść )

pomocy: w punktach calkowitych tez pochodna nie istnieje a jak zrobic to bez rownosci {x}=x−[x] ?

pomocy: ?

pomocy: ?

Godzio:

{x + h} − {x}
h

Znów w całkowitych x ∊ Z (nie wiem czemu wcześniej pisałem ∊ N )

{x + h} − {x}		{x} + {h} − {x}		{h}
	=		=
h		h		h

I granica znów nie istnieje. Policz sobie granicę w 0⁺ i 0⁻

pomocy: granica nie istnieje w punktach calkowitych a w pozostalych ile wynosi?

pomocy: ?

pomocy: ?

Mila: 1

wredulus_pospolitus: pomyśl trochę 'co to jest pochodna funkcji' jaka jest interpretacja geometryczna pochodnej funkcji

pomocy: a dlaczego 1 jak to wyliczyc?

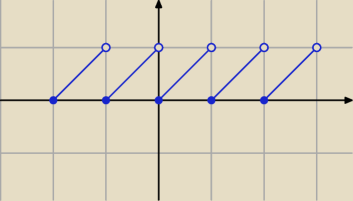
Mila: Patrząc na wykres: Masz tam dla x∉C fragmenty funkcji: f(x)=x+c c− przesunięcie , dla każdego przedziału inna stała.