prosze o pomoc raw:

	ax+2
Witam mam dość dziwne zadanie Dana jest funkcja homograficzna f(x)=		. Naszkicuj
	x−b

w układzie współrzędnych zbiór wszystkich punktów (a,b) dla których ta funkcja jest malejąca w przedziałach (−∞;b),(b;∞).

raw: wie ktoś jak zrobić ?

Godzio:

a(x − b) + ab + 2		ab + 2
	=		+ a, x ≠ b
x − b		x − b

Funkcja jest malejąca w tym przedziale jeśli ab + 2 > 0 Umiesz narysować zbiór takich punktów, których to spełnia ? (wsk. a to x, b to y) ?

Bizon: skoro malejąca to znasz ćwiartki funkcji podstawowej ... znasz asymptotę pionową

raw: hmm czyli hiperbole namalować ?

Godzio: Tak, ale zbiorem punktów nie będzie hiperbola tylko ... ?

raw: asymptota pionowa to b tak ?

raw: może ktoś namalować jak to wyjdzie ?

Godzio:

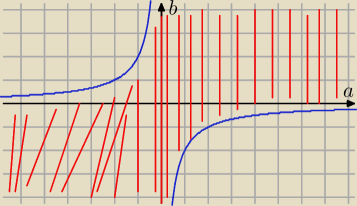
	⎧	b > − 2a dla a > 0
ab + 2 > 0 ⇒ ab > − 2 i a ≠ 0 ⇒	⎨
	⎩	b < − 2a dla a < 0

Dla a = 0 mamy 2 > 0 czyli b ∊ R − (sama oś OB − inaczej OY) Jest to obszar pomiędzy gałęziami hiperboli (bez hiperbola)

raw: okey już rozumiem dokładnie o co chodzi dziękuje !