Zad z trójkątem
Marcin: Witam, czy mógłby ktoś pomóc mi w jednym zadaniu?
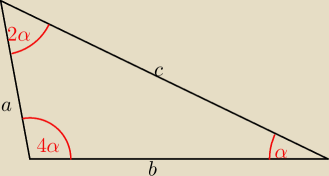
Kąty w trójkącie mają miary: α,2α,4α. Wykaż, że długości boków a,b,c tego trójkąta spełniają
równość: 1a − 1b − 1c =0.
Ja myślałem, żeby wyznaczyć a,b,c na podstawie twierdzenia cosinusów, a następnie
lewą stronę równania do wykazania przekształcić:
1a − 1b − 1c = bc−ac−aba*b*c
i wstawić tu wyliczone a,b,c, lecz to bd dużo liczenia i dlatego zastanawiam się, czy dobrze
to robię, czy może to trzeba inaczej jakoś robić
4 mar 17:23
Marcin: up
4 mar 18:06
Marcin: .
4 mar 19:22
Maslanek: Tak się zastanawiam, czy nie pomogłoby coś takiego.
Gdyby policzyć pole tego trójkąta, otrzymalibyśmy również długość promienia okręgu opisanego.
Wtedy działa twierdzenie sinusów.
Pytanie, czy dojdziemy do tożsamości, czy do jakiegoś zgrabnego wyniku

4 mar 21:56
Domel:
| 1 | | 1 | | 1 | |
| − |
| − |
| = 0 => a < b ∧ a < c |
| a | | b | | c | |
| bc − ab − ac | |
| = 0 /*abc |
| abc | |
bc − ab − ac = 0
| a | | b | | c | |
| = |
| = |
| |
| sinα | | sin2α | | sin4α | |
sin4α = sin2(2α) = 2sin(2α)cos(2α)
| b | | c | |
| = |
| |
| sin2α | | 2sin(2α)cos(2α) | |
c = 2b*cos2α
4 mar 22:20
?: wielkie dzięki

4 mar 22:44
pigor: ... , pomysł z tw. sinusów jest dobry, a więc
7α= 180
o ⇒ α=
17π i a,b,c z tw. sinusów, to wystarczy
| | 1 | | 1 | | 1 | |
wykazać, że |
| − |
| − |
| =0 ⇔ |
| | sin17π | | sin27π | | sin47π | |
⇔ sin
27π* sin
47π − sin
17π* sin
47π − sin
17π* sin
27π =0 ⇔
⇔ i dalej może spróbuj sam,
a jak nie dasz rady, to mogę spróbować jutro pociągnąć to dalej .

4 mar 23:22
MissN: Pigor skąd dokladnie sie wzielo pierwsze rownanie u Ciebie? Z tw. sinusów da sie wyznaczyć
jakiś bok za pomocą innego lub kombinowac cos z R, ale skąd to pierwsze równanie?
Chodzi mi o rownanie po wystarczy wykazać, że...
23 mar 20:48
pigor: | | a | | b | | c | |
... z tw. sinusów |
| = |
| = |
| = 2R |
| | sinα | | sinβ | | sinγ | |
a= 2Rsin
17π, b= 2Rsin
27π, c= 2Rsin
47π,
zatem z równania :
| 1 | | 1 | | 1 | | 2R | | 2R | | 2R | |
| − |
| − |
| = 0 /*2R ⇔ |
| − |
| − |
| = 0 ⇔ |
| a | | b | | c | | a | | b | | c | |
| | 1 | | 1 | | 1 | |
⇔ |
| − |
| − |
| = 0 itd. |
| | sin17π | | sin27π | | sin47π | |
23 mar 21:43
T: sin2/7π* sin4/7π − sin1/7π* sin4/7π − sin1/7π* sin2/7π =0 nie mogę tego rozwiązać ;c
6 gru 19:51
misiak:
α+2α+4α=180
o
3α+4α=180
o −−−−> sin3α=sin(180
o−4α)=sin4α
i teraz:
| 1 | | 1 | | 1 | |
| − |
| − |
| =0 |
| sinα | | sin2α | | sin4α | |
| | 1 | | 1 | | sin4α+sin2α | | 2sin3α*cosα | |
ale |
| + |
| = |
| = |
| = |
| | sin2α | | sin4α | | sin2α*sin4α | | 2sinα*cosα*sin4α | |
| 2sin4α*cosα | | 1 | |
| = |
| |
| 2sinα*cosα*sin4α | | sinα | |
6 gru 20:15
T: Dziękuję, stawiam piwo

6 gru 20:32




