funkcja
Paulina:
Naszkicuj wykres funkcji f(x) || f (x) = |4|x| − 4| . Na podstawie wykresu określ
przedziały, w których funkcja jest rosnącą
Najpierw muszę f(x)=4x−4 ?nie wiem co z tym modułem mam zrobić ?
4 mar 16:53
ICSP: f(x) = 4x
f(|x|) = 4|x|
4 mar 16:56
Paulina:
Nie bardzo mi szły funkcję możesz wytłuamczyć ? To jest odbicie względem osi OY ?
4 mar 16:57
ICSP: Rysujesz wykres dla x dodatnich. Jak już będzie gotowy dla x > 0 odbijasz go symetrycznie
względem osi OY i dostajesz dla x < 0
4 mar 17:00
Paulina:
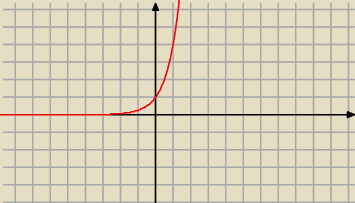
Mam 4
x teraz to co po lewej na prawą ?
4 mar 17:02
ICSP:
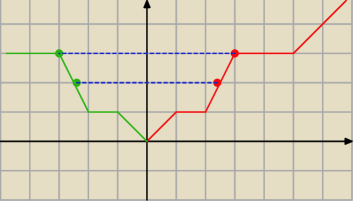
czerwony − wykres pewnej funkcji f(x) narysowany tylko dla x > 0
Teraz odbijam go symetrycznie względem osi OY i dostaje f(|x|)
4 mar 17:06
ICSP: Jeżeli narysujesz sobie jakiś wykres f(x) leciutko na kartce długopisem (dla x > 0) . Następnie
zegniesz kartkę wzdłuż osi OY i poprawisz ten wykres jakimś mocnym flamastrem to dostaniesz
f(|x|)
4 mar 17:07
Paulina: To otrzymam parabole a le nie rozumiem co z tym kawałkiem po lewej ?
4 mar 17:09
ICSP:
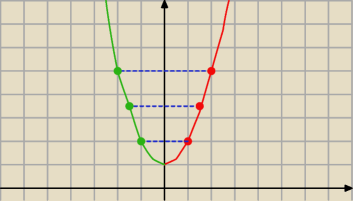
Może to coś przypomina parabolę, ale niestety nie można tego tak nazwać

4 mar 17:12
Paulina:
Czyli to co po lewej stronie przed odbiciem wgl mnie nie interesuję ?
4 mar 17:13
ICSP: W ogóle. Rysujesz tylko dla x > 0 Odbicie załatwi resztę.
4 mar 17:15
Paulina:
Dziękuję Ci

4 mar 17:15
Paulina:
f(x)=|log1/3|x+2|| a to ?
4 mar 17:18
Paulina: ?
4 mar 17:25
Paulina: ?
4 mar 17:56
Mila:
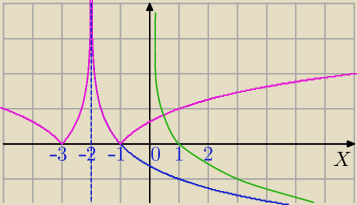
1) rysujesz wykres funkcji
g(x)=log(1/3)x
2) Translacja o wektor [−2,0]⇒
h(x)=log(1/3)(x+2)
3) symetria wykresu względem prostej x=−2⇒
h(x)=log(1/3)(|x+2|)
4)symetria względem OX dla y<0⇒
f(x)=|log(1/3)(|x+2|)
4 mar 18:10
Paulina:
Czemu symetria względem prostej x=−2 ?
4 mar 18:13
Mila:
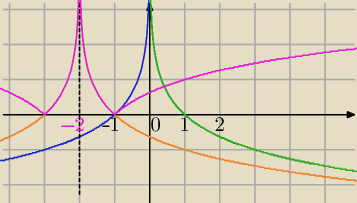
To tłumaczył CI
ICSP
Możesz zacząć inaczej;
y=log
(1/3)x⇒S
OY⇒y=log
(1/3)|x|⇒T
[−2,0]⇒y=log
(1/3)|x+2|⇒S
OX dla y<0⇒
y=|log
(1/3)|x+2||
i masz to samo.
4 mar 18:31
Paulina:
Tamto zadanie zrozumiałam bo miałam |x| a tutaj mam |x+2| ?
4 mar 18:33
Mila:
|x|=|x−0| odbicie względem prostej x=0
|x+2|=|x−(−2)| odbicie wzgledem prostej x=−2
Możesz robić II sposobem 18:31 i masz wg sposobu , który zrozumiałaś.
4 mar 18:39
Paulina:
Mogłabyś mi podać kilka przykładów do przećwiczenia ?
4 mar 18:42
Mila:
1) f(x)=x2−2|x|+3
2) f(x)=log2|x−1|
3) f(x)=log2|x|
4 mar 18:50
Paulina:
c) log2|x| czli rysuję log2x a potem odbijam na prawą stronę
b) log2 przesuwam o wektor [1,0] i odbijam względem prostej x=1
a) tu bym rysowała w przedziałach (−∞,0) i <0,∞)
4 mar 19:24
Mila:
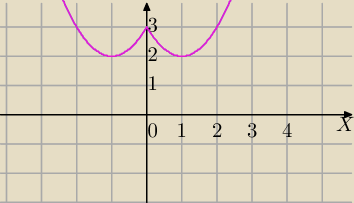
f(x)=x
2−2|x|+3
a) rysujesz wykres g(x)= x
2−2x+3 tylko dla x≥0 i symetria względem OY.
4 mar 19:59
Paulina:
A pozostałe są ok? Muszę te przekształcenia ogarnąć. Proste przykłady zrozumiałam a na maturze
zawsze jest zadania z wykresem funkcji.
4 mar 20:01
Mila:
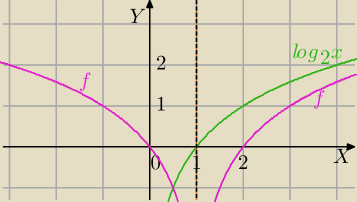
b)f(x)=log
2|x−1|
y=log2x⇒T
[1,0]⇒
y=log2(x−1)⇒S
x=1⇒
f(x)=log2|x−1|
4 mar 20:07
Paulina:
Czyli ja źle rozpisałam ?

4 mar 20:09
Mila:
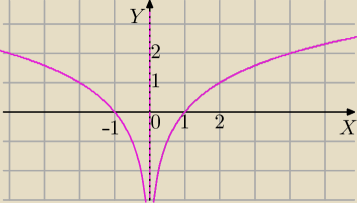
f(x)=log
2|x|
3) log
2(x)⇒S
OY⇒f(x)=log
2|x|
4 mar 20:10
Paulina:
Jak tutaj rysować takie piękne wykresy ?
4 mar 20:11
Mila:
Opcja rysuję.
4 mar 20:15
Paulina:
Ale jak wpisuję log2 to nie mogę narysować ?
4 mar 20:15
Mila:
2) Miałaś dobrze.
3) Pomyliłaś strony. Na lewą stronę odbijamy.
4 mar 20:17
Mila:
Wpisz tak:
ln(x)/ln(2)
4 mar 20:21
Paulina:
Jak mogę prosić o pomoc to byłabym Ci wdzięczna.Dosłownie 10 zadań

4 mar 20:25
Paulina:
| | 2 | |
1. Naszkicuj wykres funkcji f(x)= |
| |
| | |x+3|−1 | |
Wiem, że w przedziale ale potem trzeba narysować niezamalowane kółeczka ?
4 mar 21:52
Paulina: ?
4 mar 22:10
Paulina: Mila pomożesz tylko albo aż 10 tych przykładów ?
4 mar 22:22
Paulina: ?
4 mar 23:10
Mila:
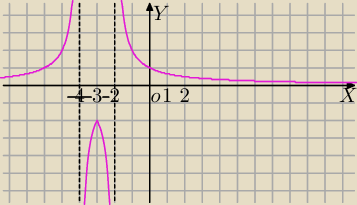
Tu najlepiej rozpisać.
D:
|x+3|−1≠0
|x+3|≠1⇔x+3≠1 i x+3≠−1
x≠−2 i x≠−4
===========
|x+3|=x+3 dla x≥−3 i x∊D
wtedy masz wzór:
| | 2 | | 2 | |
f(x)= |
| ⇔f(x)= |
| |
| | x+3−1 | | x+2 | |
x=−2 asymptota pionowa
dla
x<−3 i x∊D
x=−4 asymptota pionowa
4 mar 23:47
Paulina:
Dziękuję, jutro jeszcze zapytam

5 mar 00:03
Mila: 
5 mar 00:19
Paulina:
Czyli to zostało namalowane w dwóch przedziałach ?
5 mar 16:25
Paulina: ?
5 mar 16:48
Paulina: ?
5 mar 17:10
Paulina:
odpowie ktoś chcę się upewnić.
5 mar 18:03
Mila:
Paulino, masz tam napisane jaki wzór ma f(x)
1) dla x≥−3
2)dla x<−3 i narysowane wykresy w tych przedziałach.
5 mar 18:05
Paulina:
Dziękuję.
5 mar 18:10
Mmmm: γ=log1/2x +2
Y=log1/3 − 1
Y=log2 (x+3)
Y=log3 (x−2)
Y=log2 x+3
29 mar 16:42
Mmmm: Pomogl by ktoś?
29 mar 16:42
 Mam 4x teraz to co po lewej na prawą ?
Mam 4x teraz to co po lewej na prawą ?
 czerwony − wykres pewnej funkcji f(x) narysowany tylko dla x > 0
Teraz odbijam go symetrycznie względem osi OY i dostaje f(|x|)
czerwony − wykres pewnej funkcji f(x) narysowany tylko dla x > 0
Teraz odbijam go symetrycznie względem osi OY i dostaje f(|x|)
 Może to coś przypomina parabolę, ale niestety nie można tego tak nazwać
Może to coś przypomina parabolę, ale niestety nie można tego tak nazwać

 1) rysujesz wykres funkcji
g(x)=log(1/3)x
2) Translacja o wektor [−2,0]⇒h(x)=log(1/3)(x+2)
3) symetria wykresu względem prostej x=−2⇒h(x)=log(1/3)(|x+2|)
4)symetria względem OX dla y<0⇒f(x)=|log(1/3)(|x+2|)
1) rysujesz wykres funkcji
g(x)=log(1/3)x
2) Translacja o wektor [−2,0]⇒h(x)=log(1/3)(x+2)
3) symetria wykresu względem prostej x=−2⇒h(x)=log(1/3)(|x+2|)
4)symetria względem OX dla y<0⇒f(x)=|log(1/3)(|x+2|)
 To tłumaczył CI ICSP
Możesz zacząć inaczej;
y=log(1/3)x⇒SOY⇒y=log(1/3)|x|⇒T[−2,0]⇒y=log(1/3)|x+2|⇒SOX dla y<0⇒
y=|log(1/3)|x+2||
i masz to samo.
To tłumaczył CI ICSP
Możesz zacząć inaczej;
y=log(1/3)x⇒SOY⇒y=log(1/3)|x|⇒T[−2,0]⇒y=log(1/3)|x+2|⇒SOX dla y<0⇒
y=|log(1/3)|x+2||
i masz to samo.
 f(x)=x2−2|x|+3
a) rysujesz wykres g(x)= x2−2x+3 tylko dla x≥0 i symetria względem OY.
f(x)=x2−2|x|+3
a) rysujesz wykres g(x)= x2−2x+3 tylko dla x≥0 i symetria względem OY.
 b)f(x)=log2|x−1|
y=log2x⇒T[1,0]⇒y=log2(x−1)⇒Sx=1⇒f(x)=log2|x−1|
b)f(x)=log2|x−1|
y=log2x⇒T[1,0]⇒y=log2(x−1)⇒Sx=1⇒f(x)=log2|x−1|

 f(x)=log2|x|
3) log2(x)⇒SOY⇒f(x)=log2|x|
f(x)=log2|x|
3) log2(x)⇒SOY⇒f(x)=log2|x|

 Tu najlepiej rozpisać.
D:
|x+3|−1≠0
|x+3|≠1⇔x+3≠1 i x+3≠−1
x≠−2 i x≠−4
===========
|x+3|=x+3 dla x≥−3 i x∊D
wtedy masz wzór:
Tu najlepiej rozpisać.
D:
|x+3|−1≠0
|x+3|≠1⇔x+3≠1 i x+3≠−1
x≠−2 i x≠−4
===========
|x+3|=x+3 dla x≥−3 i x∊D
wtedy masz wzór:

