. Ada: oblicz pole figury opisanej warunkami 4≤x²+y²≤2|x|+2|y| rozbiłam sobie to na 2 nierówności 4≤x²+y² i 2|x|+2|y|≥4 rozwiązać to graficznie? bo nie mam pomysłu

Ada: ?

Ada: ?

Ada: proszę o pomoc

Mila: 4≤x²+y²≤2|x|+2|y| ⇔ 4≤x²+y² i x²+y²≤2|x|+2|y| ⇔ x²+y²≥2² i 1⁰ x≥0 i y≥0 to x²−2x+y²−2y≤0⇔ (x−1)²−1+(y−1)²−1≤0⇔(x−1)²+(y−1)²≤(√2)² analogicznie rozażaj w pozostałych ćwiartkach.

Ada: jejuu dzięki wielkie

Mila:

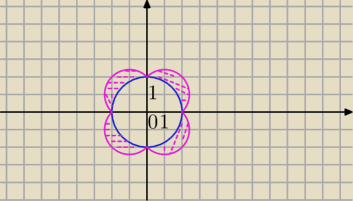
PW: "Lewa" nierówność oznacza zewnętrze koła o środku (0,0) i promieniu 2 z brzegiem. "Prawą" nierówność zapisać jako |x|² − 2|x| + |y|² − 2|y| ≤ 0 |x|² − 2|x| + 1 + |y|² − 2|y| + 1 ≤ 2 (|x| − 1)² + (|y| − 1)² ≤ 2 − w zależności od ćwiartki układu współrzędnych rysować odpowiednie fragmenty różnych kół. Obie nierówności muszą być spełnione jednocześnie (i "lewa" i "prawa"), a więc interesuje nas część wspólna. zewnętrza koła i czterech fragmentów wnętrz kół.

PW: Mila, nie widziałem Twojego wpisu − a takiego ładnego rysunku nie umiem