WsiP matura próbna matematyka 2 zad Aerodynamiczny: http://www.wsip.pl/upload/2014/02/matematyka_pp_arkusz.pdf Zad 27 i 29. Niby je zrobiłem, ale nie jestem pewny czy dobrze. Rozwiązałby ktoś od początku do końca? Z góry dzięki.

FHA: 27. Widać tutaj że bedziesz korzystał ze wzorów skróconego mnozenia. Wpierw polecam zbadać to: a²+2b²+c²≥2b(a+c) a²+2b² +c² ≥ 2ba + 2bc a²+2b² +c² − 2ba − 2bc ≥ 0 Dowód: (a−b)² + (b − c )² ≥ 0 Wystarczy rozwiązać 29. Wpisz w okrąg kwadrat. Zaznacz na okręgu punkt . Widzisz 2 trójkąty prostokątne? − Twierdzenie Następnie z tw. PITAGORASA

Aerodynamiczny: Z tym 27 to zawaliłem nie zauważyłem tych wzorów, skomplikowałem sobie tylko . A w 29 nie widzę kątów prostych.

Aerodynamiczny: Ja w 29 wrzuciłem punkt P w jeden z wierzchołków boków, wtedy też było 8r². Po czym napisałem pewien komentarz do tego. Tylko właśnie nie wiem czy tak można było

FHA: twierdzenie

Aerodynamiczny: Jakie twierdzenie?

FHA: Kąt wpisany oparty na średnicy więc 90*

Aerodynamiczny: To nie znałem, głupia ta moja szkoła... A ten mój sposób może przejść ewentualnie?

FHA: punkt P różny od wierzchołków kwadratu.

FHA: Nie dostałeś tablic? Tam masz wypisane wzory / twierdzenia.

Aerodynamiczny: Miałem, ale jakoś im nie ufam. Ale czysto teoretycznie jak tam wstawiłem po czym napisałem fajne usprawiedliwienie tego i zależności jakieś tam dopisałem.

adam44: Wstawiłby ktoś zadanka z tej matury z poziomu rozszerzonego? Chociaż kilka Bardzo mi zależy

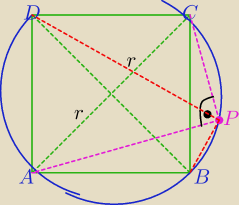
Mila: ∡APC=90^o jako kąt wpisany w okrąg oparty na średnicy |AC|. W ΔAPC: (2r)²=|AP|²+|CP|² ∡BPD=90^o jako kąt wpisany w okrąg oparty na średnicy |BD|. WΔBPD: (2r)²=|BP|²+|PD|² |AP|²+|CP|²+|BP|²+|PD|²=4r²+4r²⇔ |AP|²+|CP|²+|BP|²+|PD|²=8r²