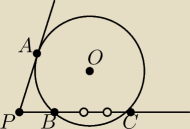
Dowód Mick: Przez punkt P poprowadzono styczną do okręgu w punkcie A i sieczną okręgu, przecinającą ten okrąg w punktach B i C. Wykaż, że jeśli |PB|BC| = 1:3, to |PB| < |AB| < BC| Proszę o pomoc i szczególowe wyjasnienie... Macie jakies recepty na dowody. Nigdy nie wiem jak je ugryźć :\

Bizon: |PA|²=|PB|*|PC} |PA|²=4|PB|² ... i wszystko jasne

Mick: Tzn.? Skorzystałeś z twierdzenia o siecznej i stycznej, tak ? Czyli |AP|² = |PB| * |BC|

Bizon: ... sprawdź to twierdzenie nie |AP|²=|PB|*|BC| tylko |AP|²=|PB|*|PC|

Mick: Fakt, mój błąd. A skąd tam Ci się wziął ten kwadrat? − 4|PB|²

Bizon: włącz myślenie − Skoro |PB|BC|=1:3 to |PC|=4|PB|

Mick: Ok teraz rozumiem

Bizon: − teraz wykazuj to |PB|<|AB|<|BC|

Mick: A jak odnieść te odcinki do odcinka |AB| ? Moze lepiej było powołać sie na podobienstwo trójkatów? Co myslisz?