jerey: wykazac ze jezeli ramoiona AD i BC trapezu ABCD o podstawach AB i CD zawierają się w prostych prostopadłych to |AB|²+|CD|²=|AC|²+|BD|²

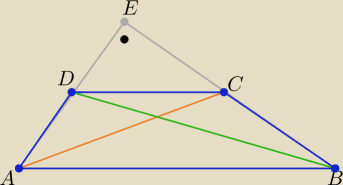Eta: z tw. Pitagorasa w ΔDCE |CD|²=|DE|²+|EC|² w ΔABE |AB|²=|AE|²+|BE|² dodając stronami + −−−−−−−−−−−−−−−− |AB|²+|CD|²= |DE|²+|EB|²+ |AE|²+|EC|² i z tw. Pitagorasa w ΔACE i ΔBDE |DE|²+|EB|²=|BD|² i |AE|²+|EC|²=|AC|² to: |AB|²+|CD|²= |AC|²+|BD|²