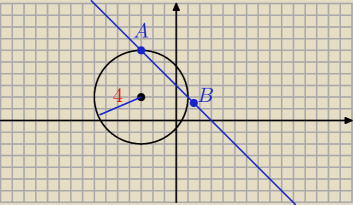
Oblicz długość cieciwy którą okrąg ośrodku S =(-3, 2) i promieniu r =4 wyznacza
Wiola: Oblicz długość cieciwy którą okrąg ośrodku S =(−3, 2) i promieniu r =4 wyznacza na prostej
y=−x+3
Antek:
Rownanie okregu w postaci kanonicznej jest takie
(x−a)
2+(y−b)
2=r
2
Naz okrag bedzie mial postac
(x−(−3))
2+(y−2)
2=4
2
(x+3)
2+(y−2)
2=16
Teraz musisz wyznaczyc punkty przeciecia sie okregu z prosta . czyli do rownania okregu za y
wstawiasz −x+3
Wyliczasz z tego x
sy i te x
sy podsatwiasz do rownania prostej i wyliczaz y
ki
Beda to punkty A i B
Ze wzoru na dlugosc odcinka liczysz odcinek AB i koniec zadania
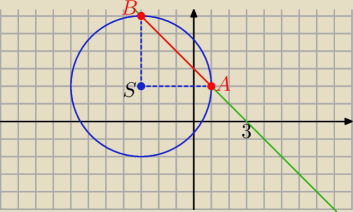 |AB|=4√2
|AB|=4√2
 Rownanie okregu w postaci kanonicznej jest takie
(x−a)2+(y−b)2=r2
Naz okrag bedzie mial postac
(x−(−3))2+(y−2)2=42
(x+3)2+(y−2)2=16
Teraz musisz wyznaczyc punkty przeciecia sie okregu z prosta . czyli do rownania okregu za y
wstawiasz −x+3
Wyliczasz z tego xsy i te xsy podsatwiasz do rownania prostej i wyliczaz y ki
Beda to punkty A i B
Ze wzoru na dlugosc odcinka liczysz odcinek AB i koniec zadania
Rownanie okregu w postaci kanonicznej jest takie
(x−a)2+(y−b)2=r2
Naz okrag bedzie mial postac
(x−(−3))2+(y−2)2=42
(x+3)2+(y−2)2=16
Teraz musisz wyznaczyc punkty przeciecia sie okregu z prosta . czyli do rownania okregu za y
wstawiasz −x+3
Wyliczasz z tego xsy i te xsy podsatwiasz do rownania prostej i wyliczaz y ki
Beda to punkty A i B
Ze wzoru na dlugosc odcinka liczysz odcinek AB i koniec zadania