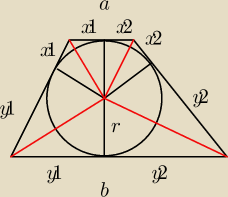
trapez opisany na okręgu włodek: Trapez ABCD o podstawach a i b jest opisany na okręgu o promieniu r. Wykaż, że 4r² ≤ ab. Było już podobne zadanie na forum jednak trapez był równoramienny i wtedy wykazywało się równość, tu jednak sprawa jest bardziej ogólna.

x2		r
	=
r		y2

r²=x₂y₂ r²=x₁y₁ ab=(x₁+x₂)(y₁+y₂)= 2r²+x₁y₂+x₂y₁ trzeba by pokazać pokazać, że x₁y₂+x₂y₁ ≤ 2r²

pigor: ..., a może chcesz ... pokombinować np. tak : r²= x₁y₁ i r²= x₂y₂ ⇒ r= √x₁y₁ i r= √x₂y₂ /2 ⇔ ⇔ 2r= 2√x₁y₁ i 2r= 2√x₂y₂ /* stronami ⇒ ⇒ 4r²= 4√x₁y₁ * √x₂y₂= 4√x₁x₂ * y₁y₂ = = 2√x₁x₂ * 2√y₁y₂ ≤ (x₁+x₂) * (y₁+y₂}=ab c.n.w. . ...