z góry dziękuje za pomoc raw: Witam W prostokącie, który nie jest kwadratem, poprowadzono dwusieczne kątów wewnętrznych i zewnętrznych. Udowodnij, że punkty przecięcia tych dwusiecznych są wierzchołkami kwadratu.

raw: mogłby ktoś spróbować rozwiązać to zadanie

raw: No drodzy ma ktoś jakiś pomysł ?// Proszę o szybką odpowiedź ,z góry dziękuje

raw: ?

Godzio: Moment, mam nadzieję, że nie jest trudne

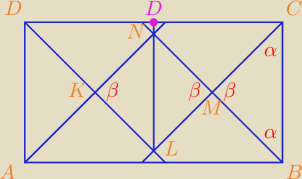
Godzio: Jasne jest, że dwusieczne kątów ∡DAB i ∡DCB oraz ∡ADC i ∡ABC są równoległe. Ponieważ są to dwusieczne to kąt α = 45^o, ponieważ suma miar kątów w trójkącie to 180^o to β = 90^o, stąd mamy, że wszystkie kąty w naszym czworokącie KLMN są równe 90^o. Pozostaje udowodnić, że długości boków są również równe. Z równoległości dwusiecznych mamy, że |KL| = |MN| oraz |KN| = |LM|. Pokażę teraz, że |MN| = |LM|. Poprowadźmy sobie odcinek LD. Utworzony trójkąt LDC ma miary kątów równe: 45^o, 90^o więc kąt ∡DLC jest równy 45^o. Skoro β = 90^o to i ∡MNL = 45^o więc trójkąt LMN jest równoramienny stąd |NM| = |LM|. Poprzez analogię mamy równość wszystkich boków co kończy dowód. Nie wiem czy dowód musiał być aż tak dokładny, ale napisałem wszystko co powinno być

raw: ooo dzięki Godzio ! jesteś wielki

raw: bardzo dobrze ,ze dokłądnie wytłumaczyłeś