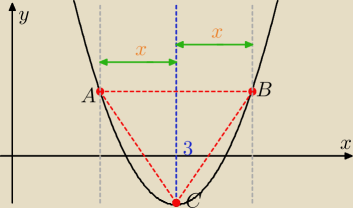
pomocy zaqwsx: wierzchołki tójkąta równobocznego ABC leżą na paraboli, będącej wykresem fukncji f(x)=x²−6x . Punkt C leży w wierzchołku paraboli. Znajdź współrzędne jednego z pozostałych wierzchołków trójkąta.

Ajtek: Punkt A spełnia warunek: A=(x; x²−6x), punkt B podobnie, oraz A i B≠x_w. Jest ich nieskończenie wiele.

Rafał28: Ajtek Tak by było ale dla trójkątów równoramiennych. −−−−−−−−−− C=(3, −9) A=(3 − x, (3−x)² − 6(3−x))=(3 − x, x² − 9) B=(3 + x, (3+x)² − 6(3+x))=(3 + x, x² − 9) |CA| = |AB| (3 − 3 + x)² + (−9 −x² + 9)² = (3−x−3−x)² + (x²−9 − x² + 9)² x² + x⁴ = 4x² x⁴ − 3x² = 0 x²(x − √3)(x + √3) = 0 x = √3 (bo x>0) −−−−−−−−−− A(3 − √3, −6) B(3 + √3, −6)

Eta: Inny sposób ( korzystam z oznaczeń na rys. Rafała prosta BC jest nachylona do dodatniej osi OX pod kątem 60^o, tg60^o=√3 BC: y= √3(x−x_C)+y_C ⇒ BC: y= √3*x−3√3−9 rozwiązując układ równań tej prostej z okręgiem: x²−6x= √3x−3√3−9 ⇒ x²−(6+√3)*x+3√3+9=0 Δ= √3 x= 3 −− to współrzędna punktu C v x= 3+√3 −− to współrzędna punktu B x_B= 3+3√3 , y_B= (3+3√3)²−6(3+√3) = ... =−6 B(3+√3, −6) Punkt A jest symetryczny do B względem prostej x=3 zatem A ma współrzędne : x_A= 2*3−(3+√3)= 3−√3 i y_A=y_B= −6 A(3−√3, −6)

Ajtek: Ups, faktycznie.

Eta: Ajtek ... to przez grypę

Ajtek: Być może, ale mam dość już. Czy π pomaga na "tą/tę laskę"

Eta: Oooo ... i to bardzo

Ajtek: To przy okazji o jakąś recepturę zapytam . Spokojnej nocki Eta

Eta: Zdrowiej Dobranoc