Zadania optymalizacyjne bbbb: Suma długości wysokości trapezu równoramiennego i obu jego podstaw jest równa s. Wyznacz tangens kąta, jaki tworzy z podstawami przekątna tego trapezu, wiedząc, że jego pole jest największe z możliwych.

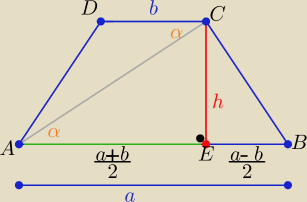
Eta: Z treści zadania : a+b+h= s ⇒ a+b=s−h

	1		a+b
P(tr)=		*(a+b)*h i |AE|=
	2		2

P(h)=0,5(s−h)*h = −0,5h²+0,5s*h −−− f. kwadratowa, parabola ramionami do dołu to osiąga maksimum dla odciętej wierzchołka:

	−0,5s
hmax=		= 0,5s , to (a+b)max= s−0,5s= 0,5s
	2*(−0,5

to |AE|= 0,25}*s

	h		0,5 s
tgα=		=		= 2
	|AE|		0,25s

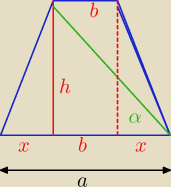
Janek191: Mamy a + b + h = s ⇒ a + b = s − h Pole trapezu P = 0,5 *( a + b)*h = 0,5*( s − h)*h = 0,5 s*h − 0,5*h² P(h) = − 0,5*h² + 0,5s*h −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	− 0,5 s
Pole jest największe dla h = p =		= 0,5 s
	− 1

wtedy a + b = s − 0,5 s = 0,5 s oraz

	a + b		0,5 s
x + b + x + b = a + b ⇒ x + b =		=		= 0,25 s
	2		2

	h		0, 5 s
tg α =		=		= 2
	b + x		0,25 s

==================================

Eta: Ciekawe? ... czym się różni to rozwiązanie od podanego przeze mnie ? chyba tylko tym: ==============================

Eta: A ... mój rysunek ładniejszy

Janek191: Jak zaczynałem, to jeszcze nie było rozwiązania Rysunek ładniejszy, bo Eta ładniejsza