planimetria

planimetria bezendu: Dany jest trójkąt prostokątny. Wykaż, że suma pól kół o średnicach będących przyprostokątnymi trójkąta jest równa polu koła o średnicy równej przeciwprostokątnej. Proszę tylko o rysunek.

2 mar 21:13

PW: To popatrz na hasło "księżyce Hipokratesa", na pewno i takie zadanie będzie.

2 mar 21:21

Mila:

2 mar 21:22

bezendu: Też bym chciał mieć taką wiedzę jak Ty. Widzisz zadania i wiesz co jak z czym połączyć a mnie te dowody z planimetrii męczą i spać nie dają i jeszcze najgorsze to, że nie wiem czy podobne będzie na maturze.

2 mar 21:24

Ajtek: Witam Mila, PW emotka

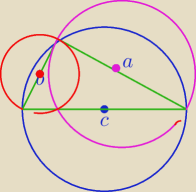
bezendu łap emotka

i nie marudź emotka

2 mar 21:26

bezendu:

	c		πc²
Pole koła dużego π(		)²=
	2		4

	πb²		πa²
A pola małych to		i
	4		4

πa²		πb²		πc²
	+		=
4		4		4

2 mar 21:30

Ajtek: Doprowadź to do tw. Pitagorasa emotka

2 mar 21:32

bezendu:

π(a²+b²)		πc²
	=
4		4

2 mar 21:34

Ajtek: No działaj dalej

2 mar 21:35

bezendu: Jakie dalej ? tu już nic nie da się zrobić ?

2 mar 21:37

Mila:

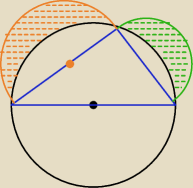
Księżyce Hipokratesa.

2 mar 21:37

bezendu: I promienie to połowy boków ?

2 mar 21:38

Ajtek: Jak się nie da

π(a²+b²)		π*c²		4
	=		/*
4		4		π

a²+b²=c², gdzie a, b przyprostokątne, c zaś przeciwprostokątna emotka

2 mar 21:39

Ajtek: Tak emotka

2 mar 21:39

bezendu: Mila tylko skąd na maturze mam wiedzieć np o tych księżycach czy innych ?

2 mar 21:40

Mila: Mogłeś tam napisać, że a²+b²=c² z tw. Pitagorasa⇔..... Tak. Δ jest prostokątny.

2 mar 21:41

Mila: Nie musisz wiedzieć, ale pola różnych takich figurek mogą być.

2 mar 21:42

bezendu: Teraz co robiłem ten arkusz to był dla mnie przystępny. A mogę zostawić tak jak 21:34 ?

2 mar 21:44

Ajtek: Nie wiem, niech Mila się wypowie. Może jakiś komentarz byłby dobry.

2 mar 21:45

Trivial: Milu, fajny misio Ci wyszedł. Tylko gdzie drugie oko...

2 mar 21:48

Mila:

2 mar 21:49

Mila: 21:34 masz uzupełnić, jak napisał Ajtek Trivial, ten misio jest z dyskontu.

2 mar 21:52

bezendu: a ten rysunek 21:49 ?

2 mar 21:54

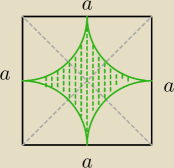
PW: bezendu, popatrz jakie ładne zadanie narysowała Mila − ta zielona gwiazdka ma pole równe polu kwadratu pomniejszonemu o 4 ćwiartki koła (moi koledzy mawiali − co sie bedziem rozdrabniać, litr koła).

2 mar 22:01

bezendu: Właśnie pytałem co to za rysunek ?

2 mar 22:02

zawodus: bardzo ładny rysunek emotka

2 mar 22:08

Mila: Masz obliczyć pole "gwiazdki".

2 mar 22:10

Ajtek: Cześć zawodus, też mi się podoba. Zadanko z poziomu gimnazjum chyba

2 mar 22:12

bezendu: Tutaj będą 4 trójkąty równoboczne ?

2 mar 22:14

Ajtek: A skąd równoboczne

2 mar 22:15

Mila: Gdzie Ty widzisz te Δ. Tam są 4 ćwiartki koła odcięte z kwadratu.

2 mar 22:16

bezendu: Pola wycinków trzeba obliczać ?

2 mar 22:18

Ajtek:

	a
Wystarczy policzyć pole koła o promieniu		.
	2

2 mar 22:19

bezendu:

	a²
P_koła=π
	4

2 mar 22:20

Mila: No i co dalej?

2 mar 22:21

bezendu:

	πa²
P_{tego zielonego}=a²−
	4

2 mar 22:24

Ajtek: A masz wątpliwości

2 mar 22:26

Mila:

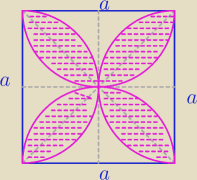
Oblicz pole koniczynki.

2 mar 22:29

Eta: Widzę artystkę emotka

2 mar 22:31

Mila: 22:24 Dobrze.

	π
S=a²*(1−		)
	4

2 mar 22:31

Ajtek: Mila zadanko z 3 klasy gimnazjum

2 mar 22:32

bezendu:

	π
To akurat wczoraj liczyłem a²(		−1) ale może być źle
	2

2 mar 22:32

Mila: Pole księżyców H też oblicz.

2 mar 22:32

Mila: 22:32 dobrze. To jednak coś widzisz .

2 mar 22:33

Antek: I jesli moge prosic to rozete czterolistna emotka

2 mar 22:34

bezendu: Tutaj może być problem.

2 mar 22:36

bezendu: ?

2 mar 22:53

zawodus: hej wszystkim emotka

bezendu szukaj półokręgów

2 mar 22:55

bezendu: Hmm ?

2 mar 22:57

Mila: Wskazówka: Δ+2 półkola o średnicach a i b.......

2 mar 23:01

bezendu:

	1		a		a²
P_Δ=		a		=
	2		2		4

	a²		πb²		πa²
P=		+		+
	4		8		8

2 mar 23:04

Mila: Boki Δ: a,b− przyprostokątne c− przeciwprostokątna.

	1
P_Δ=		a*b
	2

Dalej sam.

2 mar 23:07

bezendu:

	ab
P_Δ
	2

A czy pola tych półkuli są dobrze ?

2 mar 23:09

Mila: Dobrze pola półkoli.

2 mar 23:12

bezendu: Czyli ostatecznie

	ab		πb²		πa²
P₌		+		+
	2		8		8

2 mar 23:14

Mila: I co dalej?

2 mar 23:18

bezendu: Od pola kwadratu należy to odjąć ?

2 mar 23:19

Mila: To co Ty liczysz Bezendu?

2 mar 23:21

bezendu: To już nie wiem co mam wyliczać. Skoro policzyłem już te pola, to koniec zadania.

2 mar 23:22

Mila: Liczymy pole księżyców H. Rys. 21:37

	ab		1		1
Policzyłeś pole Δ+ 2 półkola.=P_f=		+		a²π+		b²π
	2		8		8

P_księżyców=P_f− pole półkola o średnicy c

	ab		1		1
P_księżyców=		+		a²π+		b²π−.......?
	2		8		8

2 mar 23:26

bezendu: −pole koła o średnicy c tak ?

2 mar 23:30

Mila: tak..

2 mar 23:32

Mila: Półkola.

2 mar 23:32

bezendu:

	ab		a²π		b²π		c²π
P=		+		+		−
	2		8		8		8

2 mar 23:35

Mila: Dalej.

2 mar 23:37

bezendu:

	ab
P=		+U{π(a²+b²}−c²π}{8}
	2

	4ab		πc²−πc²
P=		+
	2		8

P=2ab ?

2 mar 23:39

Radek: Dobry wieczór mogę mieć do Pani pytanie odnośnie tego zadania z kombintoryki z arkuszu zadania.info ? Tylko chodzi o potwierdzenie wyniku.

2 mar 23:42

Mila: Bezendu:

	a*b
P=		−0
	2

	1
P_księżyców=		ab
	2

Radek napisz które zadanie, dam Ci odpowiedź jutro, bo nie liczyłam.

2 mar 23:45

Mila: DObranoc emotka

2 mar 23:47

bezendu: Dziękuję i dobranoc. emotka

2 mar 23:48

kamil: Znależć funkcję odwrotną do podanej . Wyznaczyć dziedzinę tej funkcji oraz jej zbiór wartości f(x)=tg(3x−1) f(x)=1(1/2)3x A czy by pomógł ktoś w zadanku

widzę , że wcześniejsze skończone to wstawiam swoje

2 mar 23:55

bezendu: Nie i po drugie masz już temat w którym dostałeś wskazówki co masz robić !

3 mar 00:10

kamil: NIe mam napisane co robić tylko ktoś napisał posta o treści "i w czym problem?" to nie widzę wskazówki w tych słowach

3 mar 00:17

bezendu: To w tym temacie też nie szukaj, bo tutaj jest planimetria jak zauważyłeś.

3 mar 00:18