123
qu: 4
x − 12 * 2
x +32 >0
Podpowiedz wystarczy, sam spróbuje zrobić
2 mar 20:26
Ajtek:
4
x=(2
2)
x 
.
2 mar 20:28
kika: 4x=(2x)2 podstaw 2x=t
2 mar 20:28
Ajtek:
kika i to wszystko
2 mar 20:29
kika: t>0 i rozwiązać nierównośc , jak chcesz być dokładny
2 mar 20:32
Eta:
(2x−4)(2x−8)>0
2 mar 20:33
Ajtek:
A w matematyce jest dowolność istotna, czy dokładność?
2 mar 20:33
Antek: A qu powinien wiedziec jako maturzysta jakie ma byc t
2 mar 20:33
kika: a gdy otrzyma 2x=−4 to widać ,że fałsz.
2 mar 20:37
Ajtek:
Bądźmy konsekwentni w podpowiadaniu!
2 mar 20:38
Trivial: Ajtek, można bez założeń rozwiązać, to i tak wyjdzie w praniu...
2 mar 20:45
qu: wychodzi mi narazie, że t∊ (0:4) ∪ (8 : +∞)
2 mar 20:47
Ajtek:
Cześć
Trivial .
Ty to wiesz, ja to wiem. Nie mniej jednak, dla świętego spokoju założenie trzeba rzucić.
2 mar 20:48
kika: Ajtku ,spoko!
2 mar 20:48
qu: co dalej ... ?
2 mar 20:50
qu: x= 3 lub x=2 tyle narazie wiem
2 mar 20:51
Trivial:
x = log2(t)
i wyznaczyć obraz (zbiór wartości) dla t ∊(0, 4)∪(8, +∞)
2 mar 20:53
qu: nie wiem czy dobrze ale zamieniłem
t na x
wyszło mi coś takiego
x∊ (0:1)∪(1:2)∪(3: +∞)
2 mar 21:03
Trivial:
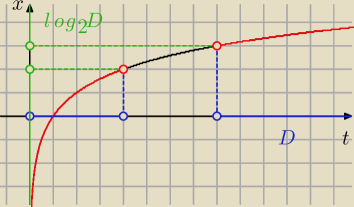
Jak "zamieniłeś"? Wynik jest niepoprawny.
Najpierw robisz podstawienie. W dziedzinie zmiennej
t dużo łatwiej jest rozwiązać
nierówność. Powiedzmy, że wynikiem jest zbiór D. Teraz musisz jeszcze "odwrócić" podstawienie.
W tym wypadku jest prosto, gdyż istnieje funkcja odwrotna x = log
2(t). Wystarczy wyznaczyć
jej zbiór wartości dla t∊D, a wtedy będzie: x∊log
2(D)
log
2(D) to zapis na zbiór wartości funkcji log
2 na dziedzinie D.
Odpowiedź: x∊(−∞,2)∪(3,+∞
)
2 mar 21:13
qu: zrobiłem błąd w zadaniu
f(x)= log
x (4
2 − 12 *2
2 +32)
Teraz warunki dochodzą
x rózny od 1
i x>0
Mój wynik w tym przypadku bd się zgadzał
2 mar 21:17
Ajtek:
qu nie ma to jak przepisać część zadania
2 mar 21:19
Trivial: Jeżeli tam jest 4
x, 2
x to wynik będzie OK.
2 mar 21:21
qu:
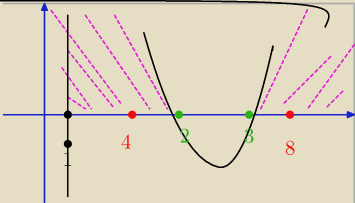
2
x =t
t=8 czyli 2
3=8 x=3
t=4 x=2
moze byc ?
2 mar 21:26
qu: sory za rysunek
2 mar 21:27
qu: Jak wy tak ładnie rysujecie ?
2 mar 21:29
Trivial: Poćwicz.
2 mar 21:30
Trivial: W szczególności przydatną opcją jest "układ współrzędnych" oraz "y = wzór(x)".
2 mar 21:32
Eta:
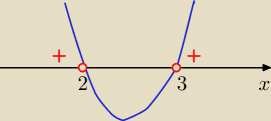
Jak wyżej podałam
4
x−12*2
x+32>0 ⇔(2
x−4)(2
x−8)>0 ⇔ odp:
x∊(−∞, 2) U (3,∞)
2 mar 21:37
Ajtek:
Eta jak się okazuje f. wyjściowa wyglądała tak:
f(x)= logx (4x−12*2x +32)
Zerknij na mój komentarz z 21:19
2 mar 21:42
Eta:
Ja
duchem nie jestem
2 mar 21:47
Ajtek:
Etuś wiem o tym
.
2 mar 21:48
Ikksa: 4x3−3x2−64x
30 paź 20:28