Planimetria
michael :
W trójkąt prostokątny o przyprostokątnych długości 5 i 12 wpisano okrąg.
Oblicz promień r tego okręgu oraz długości odcinków, na które przeciwprostokątna została
podzielona przez punkt styczności z tym okręgiem.
2 mar 20:17
kika:
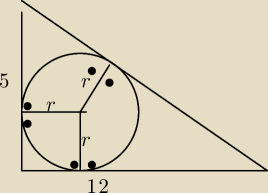
2 mar 20:26
Antek:
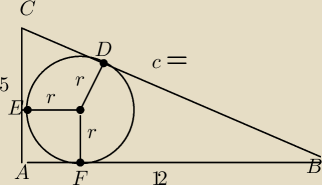
P=p*r to r=
2 mar 20:29
pigor: ..., otóż z tw. Pitagorasa , |CD|=c= 13 , a
z tw. o dwóch stycznych do okręgu z z punktu poza nim :
|CD|=|CE|=5−r= ? i |BD|=|BF|=12−r= ?, ale
|BC|=13 ⇔ |CD|+|BD|=13 ⇔ 5−r+12−r= 3 ⇔ −2r=−4 ⇔ r=2,
więc
|CD|=5−r= 5−2=3 oraz |BD|=12−r=12−2=10 − szukane długości.
2 mar 21:04
2 mar 21:04
2 mar 21:06
Antek: P=p*r wiesz co to za wzor i co w nim oznacza ?
2 mar 21:08
michael :
P=p*r /

2 mar 21:09
Antek: | | 10 | |
No to szybko do tego doszsedles . Trzeba bylo sobie zapisac np 10=2*5 to 5= |
| |
| | 2 | |
Nie napisales co to za wzor . Jesli nie wiesz to napisz bo zaraz ide spac
2 mar 21:13
michael : zle zrobiłem to
2 mar 21:13
michael : powiedz
2 mar 21:16
Antek: a wlasnie ze 21:09 dobrze
P− to pole trojkata wiec policz sobie mas zdane przyprostokatne wiec to nie problem (no
chyba ze problem)
p− to polowa obwodu trojkata wylicz c (przyprostokatna ) i juz p mozesz policzyc
r− promien okregu wpisanego w trojkat .
Zapamietaj sobie ten wzor
2 mar 21:16
Antek: Z napisales juz 21:09 tego wzoru wylicz r
2 mar 21:17
michael : a gdzie ten wzór masz w działach?
2 mar 21:23
Antek: Popatrz na rozwiazanie pigora masz tam wszystko tylko powinno byc CB=c=13(literowka)
2 mar 21:24
michael :
122+52=c2
144+25=c2
c=√169
c=13
2 mar 21:51
michael : może ktoś mi wytłumaczyć wyliczyłem z twierdzenie Pitagorasa i co dalej
2 mar 22:02
michael : nie kumam tego zadania
2 mar 22:04
2 mar 22:12
michael : ktoś was będzie taki dobry i mi wytłumaczy pokolei
3 mar 11:44
Aga1.: a=5,b=12, c=13
a+b+c=
3 mar 12:17
3 mar 19:57
michael :
a=12
b=5
c=13
p
o=15
3 mar 20:05
3 mar 20:16
Antek: Po ciezkich bojach ale


3 mar 20:18
michael : bo się nie poddaje choć wiem że mam braki
3 mar 20:24
michael :
gdzie na stronce jest to twierdzenie o dwóch stycznych do okręgu z z punktu poza nim :
4 mar 12:48
pigor: .... , właśnie dziwiłem się, dlaczego męczysz się idąc "swoją drogą",a moje
... olałeś

, a dowód jest prosty jak drut np. na twoim rysunku
|BD|=|BF|
z przystawania Δ BFO ≡ Δ BDO (cecha kbk − bok i dwa kąty do niego przylegle
są równe,) gdzie O − środek okręgu ; analogicznie masz |CD|=|CE|. ...

4 mar 13:32
michael : ktoś może mi wyjaśnić na tym forum twierdzenie o dwóch stycznych i dlaczego 5−r i dlaczedo się
odejmuje
6 mar 14:20
pigor: ...,

, a przyjrzałeś się rysunkowi
Antka 
z 2 marca 20:29; tam wszystko widać to o czym piszę.
6 mar 15:16

 P=p*r to r=
P=p*r to r=



 , a dowód jest prosty jak drut np. na twoim rysunku |BD|=|BF|
z przystawania Δ BFO ≡ Δ BDO (cecha kbk − bok i dwa kąty do niego przylegle
są równe,) gdzie O − środek okręgu ; analogicznie masz |CD|=|CE|. ...
, a dowód jest prosty jak drut np. na twoim rysunku |BD|=|BF|
z przystawania Δ BFO ≡ Δ BDO (cecha kbk − bok i dwa kąty do niego przylegle
są równe,) gdzie O − środek okręgu ; analogicznie masz |CD|=|CE|. ... 
 , a przyjrzałeś się rysunkowi Antka
, a przyjrzałeś się rysunkowi Antka  z 2 marca 20:29; tam wszystko widać to o czym piszę.
z 2 marca 20:29; tam wszystko widać to o czym piszę.