 Dylemat. prawdopodobienstwo
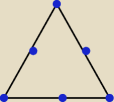
przy stole w ksztalcie tr. rownobocznego siada 6 osob { A,B,C,D,E,F } OBLICZ PRAWDOPODOBIENSTWO
ze osboy A i B usiada obok siebie.
Czy bedzie wtedy rowne Ω = 5! ? ( lub 6! ale wtedy kombinacje mnoze przez 6 )
Dylemat. prawdopodobienstwo
przy stole w ksztalcie tr. rownobocznego siada 6 osob { A,B,C,D,E,F } OBLICZ PRAWDOPODOBIENSTWO
ze osboy A i B usiada obok siebie.
Czy bedzie wtedy rowne Ω = 5! ? ( lub 6! ale wtedy kombinacje mnoze przez 6 )
| |X| | 12•4! | 12 | 2 | |||||
P(X) = | = | = | = | . | ||||
| |Ω| | 6! | 5•6 | 5 |
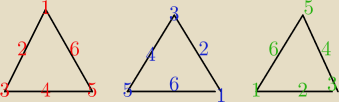 wszystkie 3 obrazki przedstawiaja identyczne roztawienie tych 3 osob, wiec Ω = 6! / 3 ?
wszystkie 3 obrazki przedstawiaja identyczne roztawienie tych 3 osob, wiec Ω = 6! / 3 ?
