Twierdzenie sinusów Loki: W trójkącie ABC mamy dane |AB| = 12 |BC| = 6√2 |AC| = 6(1 + √3) oraz |kąt BAC| = 30° . Oblicz miary pozostałych kątów trójkąta. |kąt BAC| = 30° = α = sinα= 1/2 Obliczyłem to tak: 12 / sinγ = 6√2 / 1/2 sinγ = √2 / 2 = 45° β = 180 − 45 − 30= 105° A teraz moje pytanie: 1) Chciałbym obliczyć sinβ takim sposobem: 6√2 / α = 6(1 + √3) / sinβ jak to zrobić ? Doszedłem do wyniku: √2 (1 + √3) / 4 Nie mam pomysłu co mam zrobić z tym działaniem aby sinβ = 105°.

Loki: Wie ktoś ?

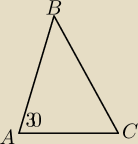
ccc: |AB| = 12 |BC| = 6√2 |AC| = 6(1 + √3 Z tw. cosinusów: IACI²=IABI² + IBCI² −2*IABI * IBCI * cosABC

Antek: sin105= sin(60+45) a na to jest wzor sin(x+y)

Loki: Antek jeżeli coś to pomyliłeś pojecie wzoru redukcyjnego: sin(90 + 15)

ccc: Jeśli chcesz policzyć sin105 to ze wzoru z tablic sin(a+b)=sinacosb+cosasinb

Antek: Jesli tak twierdzisz . ja sin 60 i 45 znam i policze sin105 Bardzo watpie bys znal sin 15 ile wynosi .ja policze bo zastosuje wzor polokowy bo sin 30 znam ale czy TY znasz ten wzor Chociaz sin15=sin(45−30) ale wtedy bedziesz musial liczyc dwa razy

Antek:

	√6−√2
Tak do wiadomosci sin15=
	4

loki: dzięki