czworokąty Noname: zadanie 1 : Oblicz pole i obwód równoległoboku, w którym dłuższy bok wynosi 2√3, a krótsza przekątna o długości 6, tworzy z jego krótszym bokiem kąt prosty. zadanie 2 : wysokość i krótsza podstawa trapezu różnoramiennego mają długość 3. Oblicz jego pole i obwód wiedząc że kąty przy podstawie mają miarę 60 stopni i 30 stopni. zadanie 3 : znajdź wysokość rombu o boku równym 13 i przekątnej 24 Z góry dziękuję za pomoc

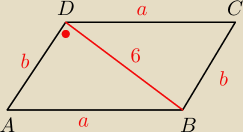
Janek191: a = ?

Noname: czyli pole wyniesie 6 √3 a obwód 12 √3 ?

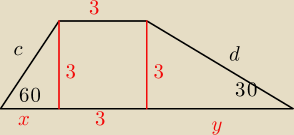
Janek191: Mamy

3
	= tg 60o = √3 ⇒ x = √3
x

3
	= sin 30o = 0,5 ⇒ d = 6
d

y		√3
	= cos 30o =
d		2

y		√3
	=		⇒ y = 3√3
6		2

c² = (√3)² + 3² = 3 + 9 = 12 = 4*3 ⇒ c = 2√3 Pole trapezu P = 0,5*( a + b)*h = 0,5*( √3 + 3 + 3√3)*3 = 1,5*( 3 + 4√3) = 4,5 + 6√3 Obwód trapezu L = a + b + c + d = ( √3 + 3 + 3√3) + 3 + 2√3 + 6 = 12 + 6√3

Janek191: z.1 Jaka jest długość dłuższego boku równoległoboku. Podane dane są sprzeczne !

pigor: w 1−szym zadaniu masz coś z danymi nie tak; czy na pewno dłuższy bok ma długość 2√3, a krótsza przekątna 6

Noname: Przepraszam ma być 2√13

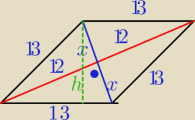
Janek191: Mamy 12² + x² = 13² x² = 169 − 144 = 25 x = 5 2x = 10 Pole rombu P = 0,5*24*10 = 120 oraz pole rombu P = 13*h 13 h = 120

	120		3
h =		= 9
	13		13

=============

pigor: ..., zad. 3. niech d − połowa krótszej przekątnej, to d²=13²−12²= 1*25 ⇒ d=5 ⇒ 2d=10, a jeśli h=? szukana wysokość rombu, to np. z porównania wzorów na pole rombu masz równanie 13*h= ¹₂*24*10 ⇒ 13h= 120 ⇒ h ≈ 9,23 . ...

Noname: Dziękuję wam bardzo za pomoc

Janek191: Do z. 1 a = 2√13 więc b² = a² − 6² = ( 2√13)² − 36 = 4*13 − 36 = 16 b = 4 Pole P = 2*6* b = 12 * 4 = 48 Obwód L = 2a + 2 b = 2* 2 √13 + 2*4 = ...