funkcja z parametrem
Seb: f(x) = |x2 − 2|x||. Wyznacz liczbę rozwiązań rówania y = m w zależności od parametru m.
2 mar 12:38
J: Narysuj wykres funkcji f(x) = x2 − 2IxI , potem odbij go względem osi OX,przesuwaj linijkę
równolegle do osi OX i odczytuj liczbę rozwiązań ( w ilu punktach linijka przecina Twój
wykres, w zalezności od m )
2 mar 12:57
Seb: Ja najpierw narysowałem x2 − 2x, później wartość bezwzględna, a na końcu zostaje ten
środkowy x w wartości bezwzględnej. Wychodzą mi max 4 rozwiązania, a w odp jest 6. Mógłby ktoś
sporządzić rysunek dla rozjaśnienia?
2 mar 13:31
Antek:
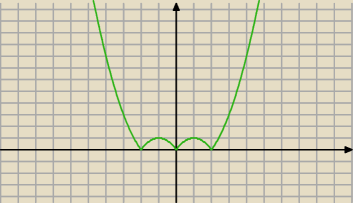
2 mar 13:37
J:
Dla x≥0 funkcja ma postać: f(x) = x2 − 2x
Dla x<0 funkcja ma postać: f(x) = x2 + 2x
narysuj i dopiero potem odbicie względem OX.
2 mar 13:37
J: No i masz gotowy rysunek

2 mar 13:38
Antek: Ale Twoje objasnie
J bardzo pomocne aby wykonac ten rysunek

2 mar 13:50
Seb: OK dzięki za pomoc

2 mar 14:22



