Dziedzina Uczę się:

	x+1
Wyznacz dziedzinę funkcji f(x)=√log12
	9−x2

pierwiastek jest pod całością.

Lorak: 9−x² ≠ 0

x+1
	>0
9−x2

	x+1
log12		≥ 0
	9−x2

Uczę się: 1^◯ x²≠9 x≠3 U x≠−3 2^o

x+1
	> 0
x2−9

(x+1)(x²−9) > 0 x³−9x+x²−9 >0 x³+x²−9x−9>0 x²(x+1)−9(x+1)>0 (x+1)(x²−9)>0 x+1>0 U x²−9>0 x>−1 U x>3 U x<−3 − tu nie wiem czy nie porąbałem znaków równości x∊(−∞,−3) U (−1,+∞) − tu nie wiem czy nie porąbałem znaków równości 3^o a z tym logarytmem nie bardzo wiem jak zrobić

Lorak: Nierówność źle rozwiązana, nieźle przykombinowałeś Z tej postaci (x+1)(x²−9)>0 możesz bezpośrednio odczytać miejsca zerowe, nie potrzeba już wymnażać, bo po wymnożeniu doszedłeś z powrotem do postaci (x+1)(x²−9). Przypomnij sobie jak rozwiązuje się nierówności wielomianowe, odsyłam tutaj: https://matematykaszkolna.pl/strona/1692.html Co do logarytmu.

	x+1
log12		≥ 0
	x2−9

prawą stronę zapisujemy przy pomocy logarytmu o tej samej podstawie

	x+1
log12		≥ log121
	x2−9

	1
Podstawa logarytmu jest równa		, więc funkcja jest malejąca, czyli odwracamy
	2

znak nierówności:

x+1
	≤ 1
x2−9

Spróbuj rozwiązać

Uczę się: x₁=−1 x₂=3 x₃=−3 i one mają być większe od 0 czyli x∊(−3,+∞) co do logarytmu

x+1
	−1≤0
x2−9

x+1		(x−3)(x+3)
	−		≤0
(x−3)(x+3)		(x−3)(x+3)

tak?

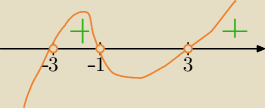
Lorak: Nierówność nadal nie jest ok. Przekształcenia przy logarytmie ok. Jest mały problem, bo pomyliliśmy się przepisując mianownik. Zamiast x²−9, powinno być −x²+9

Uczę się: to nic. zresztą w podpowiedziach jest tak: 1pkt za napisanie tych założeń. a drugi punkt jest za rozwiązanie te nierówności niewymiernej i jest napisane tak:

x+1
	>0
9−x2

a rozwiązanie tego to: x∊(−∞,−3) U (−1,3) więc nie wiem o co tu chodzi z twojego obrazka wychodzi inaczej.

Uczę się: co do logarytmu to nie wiem jak to dalej rozgryźć

wredulus_pospolitus:

x+1
	> 0 /*(9−x2)2
9−x2

(x+1)(9−x²) > 0 (x+1)(3−x)(3+x) > 0 −)(x−3)(x+1)(x+3) > 0 więc masz pierwiastki −−− x=3 , x=−1 oraz x=−3 rysujesz szkic 'metodą wężyka' ZACZYNAJĄ OD DOŁU ze względu na to, że − stoi przy najwyższej potędze. Jeżeli tak zrobisz ... otrzymasz prawidłowe rozwiązanie i drugi punkt.

Uczę się: ok zapomniałem że od prawej strony sięrysuję więc zostaje logarytm,

(x+1)−(x2−9)
	≥0
(x2−9)

zawodus: można też od lewej, ale inaczej wygląda wtedy algorytm

wredulus_pospolitus: x+1 − (x²−9) = −x²+x+10 = .... i postępujesz analogicznie do tego co wcześniej

Uczę się:

(x+1)−(x2−9)
	≥0 /*(x2−9)2
(x2−9)

x+1−(x²−9)(x²−9)≥0 x+1−(x⁴−9x²−9x²+81)≥0 x+1−x⁴+9x²+9x²−81≥0 −x⁴+18x²+x−80≥0 dobrze ja to robię?

wredulus: Bzdura ... czemu mianiownik zostal pomnozony jedynie przez czesc licznika

Uczę się: pozbywam się ułamka.

Lorak: Uczę się, wykres z 00:34 był dla (x−1)(x²−9), dlatego odpowiedź się nie zgadzała

Uczę się: ok z założenia logarytmu wyszło: (x²+x−8)(9−x²)≤0

	−1−√33
x1=
	2

	−1+√33
x2=
	2

	−1−√33		−1+√33
x∊(−∞,		> U <		,+∞)
	2		2

założenie drugie: x∊(−∞,−3) U (−1,3) i jak wyznaczyć z tego część wspólną?

	−1+√33
jest część wspólna (−1,		>
	2

ale nie widzę więcej części wspólnych a w odpowiedzi

	−1−√33		−1+√33
x∊(−∞,		> U (−1,		>
	2		2