zadanie maturalneee help ;/ mrr ;): ktoś pomoże ? nie wiem jak zrobić parę zadań zad1 dwie kule mające średnice 4cm i 1cm wpisano w stożek w ten sposób , że większa jest styczna do podstawy i powierzchni bocznej stożka , zaś mniejsza−do powierzchni bocznej stożka i do większej kuli. Oblicz pole powierzchni tego stożka zad 2 w trójkącie ABC na boku BC zaznaczono punkt D , na boku AC zaznaczono punkt E, na boku AB punkt F. Poprowadzono okręgi oA oB oC w ten sposób że okręgu oA należą punkty A,E,F , do oB − punkty B,D,F a do oc punkty C,D,E . Wykaż że trzy okręgi przecinają się w jednym punkcie

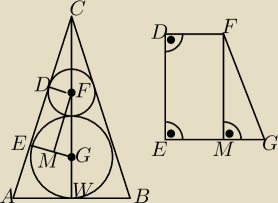Rafał28: 1. Przekrój osiowy stożka. Rysunek. |DF| = |EM| = 1 cm |MG| = |EG| − |EM| = 4 − 1 = 3 cm |FG| = 4+ 1 = 5 cm |DE| = |FM| = √5² − 3² = 4 cm −−−−−−−−−−−− Z podobieństwa trójkątów ΔCDF~ΔCEG

|DF|		|CD|
	=
|EG|		|CE|

1		|CD|
	=
4		|CD| + |DE|

1		|CD|
	=
4		|CD| + 4

	4
|CD| =		cm
	3

−−−−−−−−−−−− Z Pitagorasa

	5
|CF| = √|CD|2 + |DF|2 = √(4/3)2 + 1 =		cm
	3

H = |CW| − wysokość stożka

	5		32
H =		+ 1 + 4 + 4 =		cm
	3		3

−−−−−−−−−−−− R = |AW| = |BW| − promień podstawy stożka Z podobieństwa trójkątów ΔCDF~ΔCBW

|DF|		|CD|
	=
|WB|		|CW|

1		43
	=
R		323

R = 8 cm −−−−−−−−−−−− l = |BC| − tworząca stożka Z Pitagorasa: l = √|CW|² + |BW|² = √(32/3)² + 8² = ⁴⁰₃ cm −−−−−−−−−−−− P_c = πr(r + l) = π * 8 * (8 + ⁴⁰₃) = ⁵¹²₃ π cm²

Rafał28: 2. http://www.matematyka.pl/143696.htm