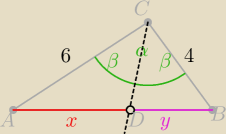
trójkąt Uczę się: W trójkącie ABC dane są |AC|=6, |BC|=4, |∡ACB|=120^◯. Wyznacz długości odcinków, na jakie został podzielony najdłuższy bok przez dwusieczną przeciwległego kąta. Wyznacz długość fragmentu dwusiecznej danego kąta zawartej w opisanym trójkącie. α=120^o β=60^o Czy dobrze to wszystko oznaczyłem na rysunku? I, że mam obliczyć x i y?

Mila: Dobrze. I jeszcze CD masz obliczyć.

bezendu: Podobne zadanie do mojego

Mila: Właśnie myślałam, abyś to rozwiązał.

bezendu: Dam inne oznaczenia |AB|=k Z tw cosinusów: k²=6²+4²−2*6*4*cos120⁰ cos120⁰=cos(180⁰−60)=−cos60⁰ k²=36+16+24 k=2√19

6		4
	=
2√19−y		y

	4√19		6√19
y=		x=
	5		5

Mila: I |CD|?

Uczę się: bezendu, zrobiłeś że:

x		4
	=
y		6

czy:

6		4
	=
x		y

i powiedz mi skąd taka zależność? co mam wpisać na necie by siędowiedzieć że takie są zależności w trójkącie?

bezendu:

	12
|CD|=
	5

bezendu: Nie znasz twierdzenia o dwusiecznej ? http://pl.wikipedia.org/wiki/Twierdzenie_o_dwusiecznej_k%C4%85ta_wewn%C4%99trznego_w_tr%C3%B3jk%C4%85cie

Uczę się: nie znałem, ale już znam...

Mila: Dobrze obliczone |CD|, bezendu. Może napisz koledze rozwiązanie z komentarzem.

bezendu: Robiłem sposobem który pokazał mi wczoraj Mila i jest genialny ! Liczysz pole trójkąta ABC a potem ΔADC+ΔDBC=ΔABC i z tego wyliczysz środkową.

Uczę się: P_ABC=6√3

Mila: Dobrze pole.

Uczę się: i teraz muszę policzyć pola ADC i DBC?

Mila: Tak.

Uczę się:

	2√204
PDBC=
	5

	3√459
PADC=
	5

jakieś kosmiczne te pola mi wyszły

Mila: Masz porównać pola, aby obliczyć |CD|. d=|CD|

1		1		1
	*6*d*sin(60o)+		*d*4*sin60o=		*6*4*sin120o
2		2		2

sin(120^o)=sin60^o 6d+4d=24 10d=24

	24		12
d=		=
	10		5

Uczę się:

	1
Jak ci taki wynik wychodzi... mogłabyś mi to rozpisać?		z 6 i 4 się skracają sin60o to
	2

	√3
		. więc nie wiem skąd taki wynik...
	2

Mila:

1		√3		1		√3		1		√3
	*6*d*		+		*4*d*		=		*6*4*		/*4
2		2		2		2		2		2

6*d*√3+4*d*√3=6*4*√3/ :√3 6d+4d=24

Uczę się: dzięki, faktycznie mianownik wychodzi 4 z mnożenia a ja obustronnie mnożyłem *2, nie zauważyłem poprostu tego dzięki, wszystko gra.

Mila: