podstawy w trapezie Nokia: Wyznacz iloczyn długości podstaw trapezu o równych ramionach, którego ramię ma długość x, a przekątna z. Prosze o pomoc.

Kaja:

	a−b
d=
	2

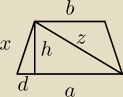
	a−b		a−b
h2+(a−		)2=z2 oraz h2+(		)2=x2
	2		2

	(a−b)2
zatem x2−		+U(a+b)2}{4}=z2
	4

x²+ab=z² ab=z²−x²

Nokia: Kaja: mogłabyś mi wytłumaczyć te ostatnie zapisy? U(a+b)2}{4}=z² z góry dzięki

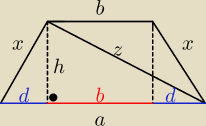
agulka: a=b+2d a−b=2d

	a−b
d=
	2

	a−b		2b+a−b		a+b
b+d=b+		=		=
	2		2		2

	a−b		(a−b)2
h2=x2−d2=x2−(		)2=x2−
	2		4

	a+b		(a+b)2
h2=z2−(b+d)2=z2−(		)2=z2−
	2		4

Skoro prawe strony są równe, to lewe też są równe:

	(a−b)2		(a+b)2
x2−		=z2−		/*4
	4		4

4x²−a²+2ab−b²=4z²−a²−2ab−b² 2ab+2ab=4z²−4x² 4ab=4(z²−x²) /:4 ab=z²−x²