 Np... tak;
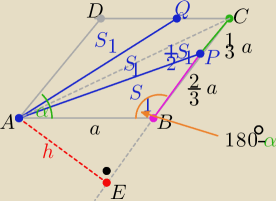
Trójkąty ABC i APC mają wspólną wysokość h= |AE|
oraz z treści zadania ( informacja o polach S)
Np... tak;
Trójkąty ABC i APC mają wspólną wysokość h= |AE|
oraz z treści zadania ( informacja o polach S)
| 1 | ||
wynika ,że S(APC)= | S(ABC) | |
| 2 |
| 2 | 1 | |||
to |AP|=2*|PC| ⇒ |AP|= | a i |PC|= | a | ||
| 3 | 3 |
| 4 | 2 | |||
|AP|2= a2+ | a2+2*a* | a*cosα | ||
| 9 | 3 |
| a | ||
|AP|2= ............. ⇒ |AP|=|AQ|= | √13+12*cosα | |
| 3 |