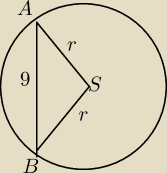
Stereometria czopo: Wycinek koła o promieniu 3 √3 po zwinięciu stanowi powierzchnię boczną stożka o wierzchołku S. Oblicz tangens kąta nachylenia tworzącej stożka do jego podstawy, jeżeli cięciwa AB ma długość 9. Ten dłuższy wycinek jest przerywaną linią w ksiązce

Tadeusz: promień podstawy stożka policzysz z obwodu ... tworzącą masz ... kąt policzysz −

pigor: ..., no cóż ... pokażę jednak, a więc np. tak : niech α − miara kąta środkowego w radianach wycinka opartego na krótszym łuku AB; R− dł.promienia podstawy stożka, to 2πR = Ł_AB ⇔ (*) 2πR= α* 3√3, gdzie np. z tw. cosinusów dla ΔABS: cosα= ... = −¹₂ ⇒ −cos(π−α)= −¹₂ /* (−1) ⇔ ⇔ cos(π−α)= cos¹₃π ⇒ π−α= ¹₃π ⇔ α=²₃π ⇒ ⇒ z (*) masz 2πR= 2π√3 ⇔ R= √3 ⇒ H²= (3√3)²−√3², gdzie H − dł. wysokości stożka ⇒ H²= 9*3−3= 8*3= 4*6 ⇒ H=2√6, więc tg β=H : R=2√6 : √3=2√2 −szukany tangens kąta .

czopo: Dziękuję za pomoc