Planimetria maramasike: 1. Dane są trzy odcinki dł.: 5, 8, 2a+3. Dla jakich wartości a z odcinków można zbudować: A) trójkąt, B) trójkąt równoramienny, C) trójkąt prostokątny? 2.Dany jest okrąg o(A,r), gdzie r=2k−1. Odl. punktu A od prostej l wynosi 10. Dla jakiej wartości parametru k prosta l: A) jest styczna do okręgu, B) nie ma punktów wspólnych z okręgiem, C) jest sieczną okręgu? 3.Do okręgu o promieniu r=5, poprowadzono trzy styczne. Każde dwie przecinają się w jednym z punktów A, B, C. Punkty te wyznaczają trójkąt równoramienny, w którym ramiona AC, BC są dwa razy dłuższe od podstawy AB. Wyznacz dł. odcinków, na jakie punkty styczności dzielą boki trójkąta. 4. W okrąg o środku O i promieniu 20 wpisano dwa okręgi styczne zewnętrznie, o środkach odpowiednio O1 i O2, z których każdy jest styczny wewnętrznie do okręgu o środku O. Jaka może być odl. między środkami O1 i O2? 5. W trapezie równoramiennym podstawy mają dł. 9 i 13. Dł. ramienia jest równa 5 cm. Oblicz odl. punktu przecięcia przekątnych tego trapezu od obu jego podstaw.

J: Zad 1) A) 2a+3 + 5 > 8 B) 2a+3 =5 lub 2a+3 =8 C) (2a+3)² = 5² + 8² lub (2a+3)² + 5²=8² lub (2a+3)² + 8² = 5²

J: W punkcie C) ostatni warunek możesz nie liczyć ( nie ma takiego a )

Ajtek: Cześć J . Należy dodać jeszcze warunek 2a+3>0

J: Cześć "Ajtek Z formalnego punktu widzenia masz absolutną rację

Domel: Nie ma to jak bon ton

maramasike: dziękuję Wam bardzo a jak rozwiązać kolejne zadania?

Ajtek: Co wiem o trójkącie równoramiennym? Co wiem o trójkącie prostokątnym?

J: Cześć "Ajtek" Zad1) już zrobione

Ajtek: Cześć J, a faktycznie . Niestety choroba daje znać o sobie.

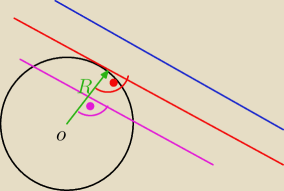
Domel: Zad. 2. Dany jest okrąg o(A,r), gdzie r=2k−1. Odl. punktu A od prostej l wynosi 10. Dla jakiej wartości parametru k prosta l: A) jest styczna do okręgu, B) nie ma punktów wspólnych z okręgiem, C) jest sieczną okręgu? ad. A) czerwona prosta ad. B) niebieska prosta ad. C) fioletowa prosta Ponieważ odległość punktu od prostej liczy się po najkrótszej drodze z punktu do prostej, w takim razie odcinek między punktem a prostą musi być prostopadły do prostej. Więc proste w zadaniu są prostopadłe do promienia łączącego środek okręgu z poszczególnymi prostymi. No to jakie możesz zapisać wzory, żeby określić czy prosta jest styczna do okręgu, nie styka się z okręgiem, lub przecina go w dwóch miejscach ? − Popatrz na rysunek i dedukuj