Geometria analityczna: wektory
V.Abel: Cześć, mam do Was kilka pytań

Bardzo liczę na Waszą pomoc

1. Na osi leżą dwa punkty stałe A i B, punkt C jest zmienny.
W jakim położeniu punktów A i B leży punkt C, jeśli stosunek wektorów λ = AC : CB wynosi:
a) 1
b) 2/3
c) jest dodatni
d) jest ujemny
2. Czy wektor można utożsamiać z jego miarą ( względną lub w ogóle)

?
Poważnie, bardzo liczę na Waszą pomoc.
28 lut 19:31
Trivial:

Wektory leżą na jednej linii, więc są tak jakby jednowymiarowe − zachowują się jak liczby.
AC = λ*CB.
A to drugie pytanie to nie wiem o co chodzi.

28 lut 19:37
zawodus : Mnie to drugie to się kojarzy z prędkością i szybkością

I jak Patrzę na matury i widzę słowo prędkość to się zastanawiam kto ich fizyki uczył

28 lut 19:44
V.Abel: Dobra ja z fizyki stałem średnio

Jaka jest różnica między szybkością, a prędkością? Żadna, tak? Czy nie?
 Trivial
Trivial, ale to jest dobra odpowiedź tylko do podpunktu a) Jakieś słowo komentarza?
P.S Moża
Mila tu zajrzy kiedyś?

28 lut 19:49
Trivial:
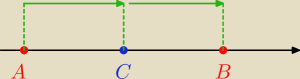
Proszę bardzo − przypadek a)
| | A+B | |
odp.: na środku, C = |
| . |
| | 2 | |
28 lut 19:49
Trivial:
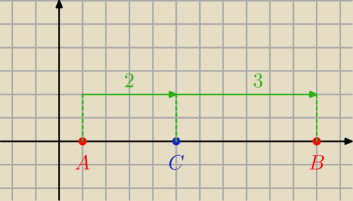
28 lut 19:53
Trivial:
c) dodatni jest gdy C leży między A,B
d) ujemny jest gdy C leży poza A,B.
28 lut 19:55
V.Abel: Trivial dzięki, ale jaką drogą doszedłeś do tego, że mamy taką, a nie inną wartość C?

28 lut 19:56
Trivial: Szczerze mówiąc to zgadywałem. Tak jest szybciej.

28 lut 20:02
Maslanek: | | s | |
Abel, szybkość −> V= |
| (iloraz drogi i czasu) |
| | t | |
| | r | |
prędkość −> V= |
| (iloraz przemieszczenia i czasu) |
| | t | |
28 lut 20:09
PW: Prawie że ścisła odpowiedź na pytanie 2. brzmi: nie.
Wektor to uporządkowana para punktów, a miara wektora to liczba (co by nie nazwał "miarą
wektora"; ja bym takiego pojęcia w ogóle nie używał). W matematyce raczej mówi się o
współrzędnej wektora (jeżeli rozpatrujemy tylko wektory na jednej prostej), ogólnie o
współrzędnych wektora przy wektorach w przestrzeni dwu− trzy − i więcej wymiarowych.
Pewnie że przy wektorach branych tylko z jednej prostej współrzędna (miara) wektora dobrze go
opisuje, gdyż po odjęciu od liczby opisującej koniec wektora liczby opisującej jego początek
otrzymamy liczbę informującą zarówno o jego długości jak i zwrocie. Wszystkie wektory mu równe
mają tę samą współrzędną (miarę). W ten sposób tworzymy klasę abstrakcji relacji równoważności
wektorów: wektor swobodny [m], gdzie m jest liczbą dodatnią, zerem lub ujemną. Jest to pewne
utożsamienie: wszystkie wektory mające współrzędną m utożsamiamy ze sobą i jednocześnie z tą
liczbą m. Gdy mówimy "wektor o mierze −7" to możemy powiedzieć: jest to np. wektor o początku
8 i końcu 1 (bo 1−8 = −7) i każdy wektor mu równy (mający tę samą miarę).
Oczekiwana odpowiedź więc zapewne brzmi: tak, można wektor na prostej (w sensie ten i wszystkie
mu równe) utożsamić z jego miarą.
Widzę, że mój elaborat jest iście prezydencki − jestem na nie, a nawet na tak.
28 lut 20:11
Trivial:
Abel, jeśli już chcesz wzorek na C dla dowolnego λ to można go wyprowadzić z zależności:
AC = λ*(CB)
A − C = λ*C − λ*B
C(λ+1) = A + λB
A,B,C to wektory od początku układu współrzędnych do punktów A,B,C.
28 lut 20:18
V.Abel: PW − dobry ten elaborat

Korzystam z książki F.Leji, bo mi tak tu kiedyś na forum polecono

(stąd pytanie o miarę)
 Trivial
Trivial a jakbyś to uzasadnił, mając na uwadze, że zawsze prawdą jest, że AB + BC = AC,
tzn, że suma miar wektorów AB, BC, AC równoległych do osi x jest zawsze (przy każdym)
położeniu równa tyle, co wyżej?
Maslanek − moja wiedza z fizyki jest powalająca, tzn jaka jest różnica między drogą, a
przemieszczeniem? To nie to samo, i tu, i tam się przemieszczasz

?
28 lut 20:54
Maslanek: Jeśli "drogę" utażsamialibyśmy z pewną krzywą, to drogą nazwiemy długość tej krzywej, a
przemieszczeniem odległość między skrajnymi jej punktami
28 lut 21:03
V.Abel: Maslanek czyli droga to długość krzywej, a przemieszczenie, jest zawsze liniowe?
Jak tak, to spoko

28 lut 21:12
pigor: ... , a ja mówię sobie krótko tak :
prędkość to wektor, a szybkość to liczba − miara tej prędkości
(długość jej wektora), dlatego dla mnie w zadaniach typu
"... od miasta A do B ... " , lub podobnych słowo prędkość nie
ma racji bytu i nie powinno się pojawić, bo to jest szybkość ,
czyli liczba odczytana z licznika np. ...

roweru, samochodu, pociągu itp....

28 lut 21:33
 Bardzo liczę na Waszą pomoc
Bardzo liczę na Waszą pomoc  1. Na osi leżą dwa punkty stałe A i B, punkt C jest zmienny.
W jakim położeniu punktów A i B leży punkt C, jeśli stosunek wektorów λ = AC : CB wynosi:
a) 1
b) 2/3
c) jest dodatni
d) jest ujemny
2. Czy wektor można utożsamiać z jego miarą ( względną lub w ogóle)
1. Na osi leżą dwa punkty stałe A i B, punkt C jest zmienny.
W jakim położeniu punktów A i B leży punkt C, jeśli stosunek wektorów λ = AC : CB wynosi:
a) 1
b) 2/3
c) jest dodatni
d) jest ujemny
2. Czy wektor można utożsamiać z jego miarą ( względną lub w ogóle)  ?
Poważnie, bardzo liczę na Waszą pomoc.
?
Poważnie, bardzo liczę na Waszą pomoc.
 Wektory leżą na jednej linii, więc są tak jakby jednowymiarowe − zachowują się jak liczby.
AC = λ*CB.
A to drugie pytanie to nie wiem o co chodzi.
Wektory leżą na jednej linii, więc są tak jakby jednowymiarowe − zachowują się jak liczby.
AC = λ*CB.
A to drugie pytanie to nie wiem o co chodzi. 
 I jak Patrzę na matury i widzę słowo prędkość to się zastanawiam kto ich fizyki uczył
I jak Patrzę na matury i widzę słowo prędkość to się zastanawiam kto ich fizyki uczył 
 Jaka jest różnica między szybkością, a prędkością? Żadna, tak? Czy nie?
Jaka jest różnica między szybkością, a prędkością? Żadna, tak? Czy nie?  Trivial, ale to jest dobra odpowiedź tylko do podpunktu a) Jakieś słowo komentarza?
P.S Moża Mila tu zajrzy kiedyś?
Trivial, ale to jest dobra odpowiedź tylko do podpunktu a) Jakieś słowo komentarza?
P.S Moża Mila tu zajrzy kiedyś? 
 Proszę bardzo − przypadek a)
Proszę bardzo − przypadek a)



 Korzystam z książki F.Leji, bo mi tak tu kiedyś na forum polecono
Korzystam z książki F.Leji, bo mi tak tu kiedyś na forum polecono  (stąd pytanie o miarę)
(stąd pytanie o miarę)  Trivial a jakbyś to uzasadnił, mając na uwadze, że zawsze prawdą jest, że AB + BC = AC,
tzn, że suma miar wektorów AB, BC, AC równoległych do osi x jest zawsze (przy każdym)
położeniu równa tyle, co wyżej?
Maslanek − moja wiedza z fizyki jest powalająca, tzn jaka jest różnica między drogą, a
przemieszczeniem? To nie to samo, i tu, i tam się przemieszczasz
Trivial a jakbyś to uzasadnił, mając na uwadze, że zawsze prawdą jest, że AB + BC = AC,
tzn, że suma miar wektorów AB, BC, AC równoległych do osi x jest zawsze (przy każdym)
położeniu równa tyle, co wyżej?
Maslanek − moja wiedza z fizyki jest powalająca, tzn jaka jest różnica między drogą, a
przemieszczeniem? To nie to samo, i tu, i tam się przemieszczasz  ?
?

 roweru, samochodu, pociągu itp....
roweru, samochodu, pociągu itp.... 