Miejsca zerowe funkcji są trzy razy większe
dominika: Miejsca zerowe funkcji g(x)=ax
2+bx+3 są trzy razy większe od miejsc zerowych funkcji
f(x)=x
2−4x+c. Wyznacz współczynniki: a, b i c, jeśli te trójmiany mają takie same zbiory
wartości.
Prosiłabym o komentarz do zadania, z góry dziękuję,
wredulus_pospolitus:
Startujemy od rzeczy podstawowych:
1) skoro mają taki sam zbiór wartości ... to a>0
2) skoro mają taki sam zbiór wartości to:
| | −(b2−12a) | | −(42 −4c | |
ywierz. g(x) = |
| = |
| = ywierz. f(x) |
| | 12a | | 4 | |
3) skoro miejsca zerowe funkcji g(x) są 3 razy większe od miejsc zerowych funkcji f(x) to:
a) x
0g1*x
0g2 = 3*x
0f1*3*x
0f2 <−−−wzory Viete'a
b) x
0g1+x
0g2 = 3*x
0f1+3*x
0f2 = 3*(x
0f1+x
0f2 <−−− wzory Viete'a
i już masz układ trzech równań z trzema niewiadomymi ... do dzieła
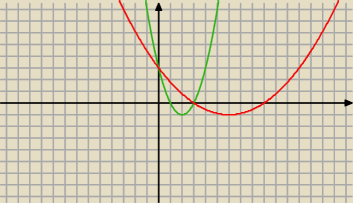... bardzo fajne zadanko
Podpowiem Ci tak −