obrot zadanie:

	π
znajdz wzor i macierz obrotu wzgledem osi oy o kat		? w R3
	2

wzor obrotu wzgledem osi oy o kat α to: x'=xcosα+zsinα y'=y z'=−xsinα+zcosα dobrze?

zadanie: moge prosic o pomoc?

Mila: Czekaj cierpliwie, aż Trivial tu spojrzy, ja nie pamiętam.

MQ:

	π
Wzasadzie dobrze, tyle, trzeba jeszcze podstawić		za α i wyliczyć.
	2

zadanie: a takie zadanie znajdz wzor i macierz rzutu na plaszczyzne x+y+z=0 wzdluz wektora (−3,4,7).

zadanie: ok dziekuje a jeszcze dla osi ox i oz wzor obrotu wzgledem osi ox o kat α to: x'=x y'=ycosα−zsinα z'=ysinα+zcosα wzor obrotu wzgledem osi oz o kat α to: x'=xcosα−ysinα y'=xsinα+ycosα z'=z a te wzory sa poprawnie?

zadanie: ?

zadanie: moge prosic o pomoc?

Trivial: 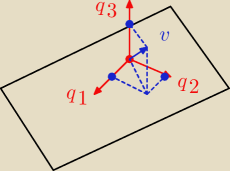http://pl.wikipedia.org/wiki/Elementarne_macierze_transformacji Nie za bardzo wiem co masz na myśli mówiąc "rzut na płaszczyznę x+y+z=0 wzdłuż wektora (−3,4,7)". Zignoruję tę czerwoną część. Płaszczyznę przechodzącą przez początek układu współrzędnych opisują dwa wektory liniowo niezależne leżące na tej płaszczyźnie. Jeżeli do tego będą ortogonalne, to problem rzutowania stanie się trywialny. Wybieramy np.: q₁ = (1, −1, 0) q₂ = (1, 1, −2) q₁∘q₂ = 1 − 1 + 0 = 0 ⇒ wektory ortogonalne. Powiedzmy, że chcemy rozłożyć dowolny wektor v na 3 wektory: q₁, q₂ i wektor q₃, który jest prostopadły do obu wektorów: q₁, q₂. Wektory (q₁, q₂, q₃) tworzą bazę przestrzeni R³, a zatem za pomocą ich kombinacji można zapisać dowolny wektor. v = c₁q₁ + c₂q₂ + c₃q₃ Biorąc obustronnie iloczyn skalarny z q_k obliczamy: q_k∘v = c₁ q_k∘q₁ + c₂ q_k∘q₂ + c₃ q_k∘q₃ Po prawej stronie zostanie tylko jedna wartość: q_k∘q_k (pozostałe wynoszą 0), zatem:

	qk∘v
qk∘v = ck qk∘qk → ck =
	||qk||2

A teraz najlepsze. Projekcją dowolnego wektora v v = c₁q₁ + c₂q₂ + c₃q₃ będzie po prostu część z q₁, q₂ (odrzucamy resztę − q₃). P(v) = c₁q₁ + c₂q₂ No to teraz trzeba policzyć współczynniki c₁, c₂ dla dowolnego wektora v i gotowe. v = (v_x,v_y,v_z)

	q1∘v		vx − vy
c1 =		=
	||q1||2		2

	q2∘v		vx + vy − 2vz
c2 =		=
	||q2||2		6

	vx − vy		vx + vy − 2vz
P(v) =		(1,−1,0) +		(1,1,−2)
	2		6

	1
=		[vx*(2,−1,−1) + vy*(−1,2,−1) + vz*(−1,−1,2)]
	3

Czyli macierz P wygląda tak: 2 −1 −1 P = ¹₃ * −1 2 −1 −1 −1 2

Trivial: Inny sposób, który zadziała w R³ to wycięcie części z q₃. Wektor q₃ odczytujemy z równania płaszczyzny (jest on wektorem normalnym): q₃ = (1,1,1).

	1
Zauważamy, że P(v) = v − c3q3, gdzie c3 =		(q3∘v)
	3

	vx+vy+vz
c3 =
	3

	1
P(v) =		[(3vx, 3vy, 3vz) − (vx+vy+vz)*(1,1,1)]
	3

	1
=		[vx*(2, −1,−1) + vy*(−1,2,−1) + vz*(−1,−1,2)]
	3

Jak widać wychodzi to samo.

Krzysiek: rzut na płaszczyznę x+y+z=0 wzdłuż wektora (−3,4,7)" czyli bierzemy dowolny punkt A=(x₁,y₁,z₁) i szukamy rzutu na płaszczyznę(ale nie rzut prostopadły tylko równoległy do wektora v=[−3,4,7]) prosta l: (x,y,z)=A+vt i szukamy punktu wspólnego prostej 'l' i płaszczyzny x+y+z=0 x₁−3t+y₁+4t+z₁+7t=0 t=1/8(−x₁−y₁−z₁) czyli szukany rzut to punkt A'=(x₁,y₁,z₁)+1/8(−x₁−y₁−z₁)[−3,4,7]= (11/8x₁+3/8y₁+3/8z₁,−4/8x₁+4/8y₁−4/8z₁,−7/8x₁−7/8y₁+1/8z₁) a macierz tego przekształcenia (A→A') to: 11/8 3/8 3/8 −4/8 4/8 −4/8 −7/8 −7/8 1/8

Trivial: Dobrze, że wyjaśniłeś, Krzysiek. Nie spotkałem się dotąd z rzutem wzdłuż wektora.

MQ: Rzuty wzdłuż wektora standardowo na polibudach liczą.

zadanie: dziekuje za pomoc

zadanie: moglbym jeszcze prosic o sprawdzenie z 18:15? i w ogole o wyjasnie tego bo jezeli chodzi o te obroty to nie wiem ktora wersje wzoru wybrac bo jest wzor na obrot o pewien kat ale tez o kat przeciwny ale kiedy jakie sie stosuje ?jak wtedy wyglada polecenie?

MQ: Dobrze

zadanie: a obrot o kat przeciwny czego dotyczy?

zadanie: Rozwazmy obrót R o kat π wzgledem prostej wzdluz wektora [1; 1; 0]. (a) Na podstawie rysunku znajdz obrazy wersorów osiowych przez przeksztalcenie R. (b) Korzystaj¡c z informacji, ze R jest przeksztalceniem liniowym, znajdz jego wzór oraz macierz. jakies podpowiedzi?

MQ: Podpowiedzią jest punkt a)

MQ: Jak się dobrze przyjrzysz temu obrotowi, to: e_x → e_y e_y → e_x oraz e_z → −e_z

zadanie: a) R jest obrotem o kat π wzgledem prostej wzdluz wektora [1; 1; 0] czyli tą prostą wyznacza wektor [1,1,0] jej rownanie to: x=t y=t z=0 R(1,0,0)= R(0,1,0)= R(0,0,1)= jak znalezc wzor tego obrotu? bo do tej pory byly obroty ae wzgledem punktu (0,0,0).

zadanie: no wlasnie nie umiem sobie tego wyobrazic jak by to narysowac?

MQ: Już ci napisałem o 23:39

zadanie: czyli R(1,0,0)=(0,1,0) R(0,1,0)=(1,0,0) R(0,0,1)=−(0,0,1) a jak wyprowadzic ten wzor? bez rysunku?

MQ: No przecież już masz: 0 1 0 1 0 0 0 0 −1

zadanie: mam jeszcze pytanie bo spotkalem sie tez z takim wzorem na obrot wzgledem osi ox x'=x y'=ycosα+zsinα z'=−ysinα+zcosα to ktory jest poprawny?

zadanie: ?

zadanie: ?