planimetria
bezendu:
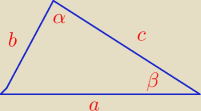
Jeden z boków trójkąta ma długość c , zaś kąty trójkąta przyległe do tego boku mają miary α i
β . Znajdź promień okręgu wpisanego w ten trójkąt
| | c2sinαsinβ | |
Za dużo obliczeń ale czy wynik to r= |
| ? |
| | sinβ+sinα+sin(α+β) | |
27 lut 19:55
zawodus: A odpowiedzi nie masz?
27 lut 19:59
bezendu:
Nie mam odpowiedzi do arkuszy.
27 lut 20:00
Godzio:
Chyba bez ten dwójki
27 lut 20:00
bezendu:
| | csinαsinβ | |
r= |
| |
| | sinβ+sinα+sin(α+β) | |
27 lut 20:01
Godzio:
27 lut 20:03
bezendu:
Dzięki
27 lut 20:05
Godzio:
A obliczeń chyba aż tak dużo nie ma
Robiłeś to przez twierdzenie sinusów ?
27 lut 20:06
bezendu:
Tak
| | 1 | |
wyznaczyłem a i b a pole za pomocą wzoru P= |
| bcsinα |
| | 2 | |
27 lut 20:10
Godzio:
Ok, bo pisząc dużo myślałem, że poszedłeś inną drogą.
27 lut 20:12
PW: Tak. Liczyłeś porównując dwa wzory na pole, do tego twierdzenia sinusów?
27 lut 20:12
bezendu:
| | csinβ | | csinβ | |
Wyznaczyłem b= |
| a= |
| |
| | sin(α+β) | | sin(α+β) | |
| | c2sinαsinβ | | 2P | |
ze wzoru na pole otrzymałem |
| i potem wzór r= |
| |
| | 2sin(α+β) | | a+b+c | |
27 lut 20:15
Mila:
Wynik 20:01 dobry.
27 lut 20:20
bezendu: Dziękuję
27 lut 20:30