Marcin:
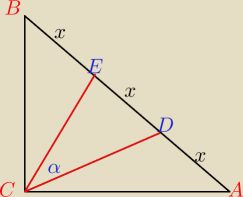
Dany jest trójkąt prostokątny równoramienny ABC.
Punkty D i E dzielą przeciwprostokątną AB na trzy odcinki równej długości.
Oblicz cosinus kąta DCE.
Czy CE i CD są równe?
27 lut 19:26
52: TAK.
27 lut 19:27
zawodus : Odpowiednie trójkąty są przystające
27 lut 19:33
Marcin: tzn? α nie jest po prostu podzielona na 3, nie?
27 lut 19:45
Marcin: tzn kąt 90, nie α
27 lut 19:46
Mila:
Kąt prosty nie jest podzielony na 3 równe kąty.
|AC|=|BC|=a
CD=|CE|
|AB|=a
√2
∡A=45
o
Oblicz |CD| z tw. cosinusów w ΔACD.
Potem jeszcze raz tw. cosinusów w ΔDCE.
27 lut 19:59
Eta:
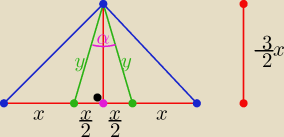
| | x | | 3x | |
y2= ( |
| )2+( |
| )2 ⇒ y2=......... |
| | 2 | | 2 | |
| | y2+y2−x2 | |
z tw cosinusów cosα= |
| = ........... |
| | 2y2 | |
27 lut 20:08
Eta:
Ooo
Mila już podała wskazówki
Nie odświeżyłam strony i nie widziałam wpisu
27 lut 20:10
Marcin: Oba rozwiązania są fajne. Dziękuję
| | 3 | |
Nie wpadłbym na to, że wysokość tego trójkąt to |
| x  |
| | 2 | |
27 lut 20:15
Eta:
Przecież kąty mają miary po 45
o , to........
27 lut 20:16
Marcin: No teraz to widzę
Dzięki
27 lut 20:18
Eta:
27 lut 20:18