Parabola Piotruś i pudel: Napisz dokładne równanie paraboli postaci y=3x² +bx +2,jeśli wiadomo że: −rzędna jej wierzchołka wynosi( −1 ) −parabola ta posiada styczną y=6x − 10

Aga1.: q=−1

	−b2+24
q=
	12

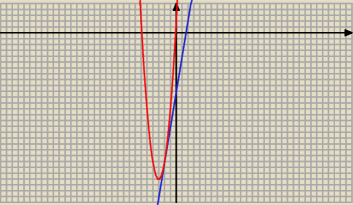
Janek191: y = 3 x² + b x + 2 y = 6 x − 10 −−−−−−−−−−− 3 x² + b x + 2 = 6 x − 10 3 x² + ( b − 6) x + 12 = 0 Δ = ( b − 6)² − 4*3*12 = ( b − 6)² − 144 = 0 ⇒ ( b − 6)² = 12² ⇒ b − 6 = 12 ⇒ b = 18 Odp. y = 3 x² + 18 x + 2 ====================

J: Rzędna wierzchołka paraboli ma być: y_w = − 1.

J: Rozwiązanie "Aga1" daje dwie wartości: b = 6 oraz b= − 6 Po sprawdzeniu okazuje się, że tylko dla b = − 6 prosta ma jeden punkt wspólny z parabolą.

Bizon: ... oj Janeczku191 ... policzyłeś coś tylko nie bardzo wiesz co.

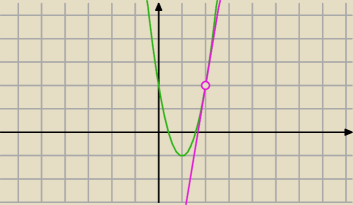
Bizon: Przyrównując wzory paraboli i stycznej znalazłeś jedną z dwóch, która jest styczna do danej prostej ... drugą pominąłeś błędnie rozwiązują równanie. Zauważ, że (b−6)²−144=0 ⇒ [(b−6)−12][(b−6)+12]=0 czyli b=18 lub b=−6 tylko parabolka, w której b=−6 spełnia założenie o rzędnej wierzchołka −

Janek191: Ja potraktowałem to jako dwa zadania

Bizon:

Bizon: ... jeśli potraktowałeś to jako dwa zadania ... to też "zgubiłeś" jedno rozwiązanie −

Janek191: Zgadza się : y = 3 x² − 6 x + 2