Planimetria Marek: Jeden z boków trójkąta jest czterokrotnie dłuższy od drugiego boku, kąt między nimi zawarty jest równy 120° a trzeci bok ma długość 21. Wyznacz długości boków.

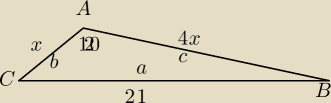
Janek191: a = 21 b = x c = 4 x α = 120^o Z tw. cosinusów mamy 21² = x² + ( 4 x)² − 2*x*4 x * cos 120^o 21² = x² + 16 x² − 8 x² * cos ( 90 + 30)^o 21² = 17 x² − 8 x² * ( − sin 30^o) 21² = 17 x² − 8 x² * ( − 0,5) 21² = 17 x² + 4 x² = 21 x² / : 21 21 = x² x = √21 ======= więc b = √21 c = 4 √21 =========================

b to b:

	1
cos120o = −		b>0
	2

	1
b to b: 212 = b2 + 16b2 + 2*b*4b*		⇒ 212 = 21b2 ⇒ b = √21 i tyle
	2