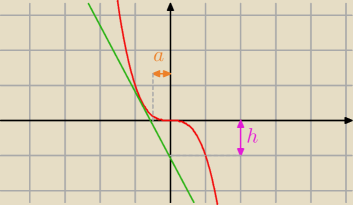
Pochodna, styczna James: W ktorym punkcie wykresu funkcji f(x)=−x³ nalezy poprowadzic styczna do tego wykresu, by pole trojkata ograniczonego ta styczna i osiami ukladu wspolrzednych bylo rowne 54?

	ah
Oznacze pole trojkata przez P=		, a − dlugosc podstawy, h − wysokosc rzucona na bok a
	2

f(x) = −x³ f'(x) = −3x² Rownanie stycznej do f(x) (w punkcie x₀): y = g(x) = −3x₀²(x − x₀) − x₀³ = x₀²(2x₀ − 3x) No i teraz a = |x_a|, gdzie x_a to argument spelniajacy rownosc g(x_a) = 0, natomiast h = |g(0)| = |2x₀³|

	2x0		2x0
g(xa) = 0 ⇔ x02(2x0 − 3xa) = 0 ⇒ xa =		⇒ a = |		|
	3		3

Zatem pozostaje rozwiazac:

	2x0   |2x03|| |   3
54 =
	2

	4x04
|		| = 108
	3

x₀⁴ = 9, skad: x₀ = √3 lub x₀ = −√3 No ale niestety w odpowiedziach mam punkty (3, f(x)), (−3, f(−3))...co tutaj robie nie tak?

James: Potrafi ktos pomoc?

James: Podbijam. Moze jednak ktos sie pokusi o sprawdzenie.

James: Hmm...juz chyba wiem co zrobilem nie tak, i blad wydaje sie dosc komiczny.

	4x04
|		| = 108 ⇔ x04 = 81... i wtedy reszta jest ok.
	3