Dla jakiej wartości parametru p funkcja f(x) = |x + 2|+|1 - x| ma dokładnie dwa
kamczatka:

Dla jakiej wartości parametru p funkcja f(x) = |x + 2|+|1 − x| ma dokładnie dwa rozwiązania,
jeśli f(x) = p
Mi wychodzi tak:
dla (−
∞;−2) f(x) = −3
dla < −2;1) f(x) = 2x+1
dla <1;+
∞) f(x) = 3
I mi nigdzie nie wychodzi że p ma dokładnie dwa miejsca zerowe.(dodaje mój rysunek) A w
odpowiedziach mam że dla p∊ (3;
∞) przyjmuje dokładnie dwa miejsca zerowe co robię źle ?
26 lut 19:28
bezendu:
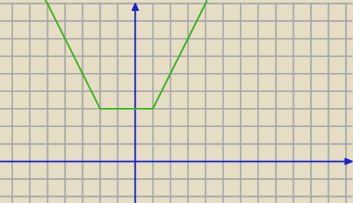
26 lut 19:33
zawodus: zły rysunek
26 lut 19:33
zawodus: tzn bezendu ma ok
26 lut 19:34
Mila:
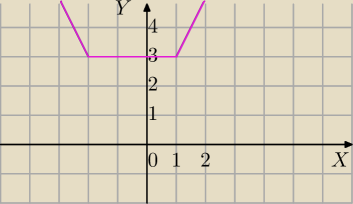
|1−x|=|x−1| z definicji wartości bezwzględnej |a|=|−a|
f(x)=|x+2|+|x−1|
|x+2|=x+2 dla x≥−2
|x−1|=x−1 dla x≥1
1) x<−2
f(x)=−x−2−x+1⇔f(x)=−2x−1
2) x∊<−2,1)
f(x)=x+2−x+1⇔f(x) =3
3) x≥1
f(x)=x+2+x−1⇔f(x)=2x+1
f(x)=m ma dokładnie dwa rozwiązania dla m>3
26 lut 19:41
kamczatka: czemu dla przedziału <−2;1)
jest x+2−x+1 a nie x+2+x−1 przecież |x−1| w tym przedziale przyjmuje wartości ujemne
26 lut 21:20
bezendu:
x∊<−2,1>
f(x)=|x+2|+|x−1|
f(x)=x+2−x+1
f(x)=3
Skoro przyjmuję wartości ujemne to opuszczając moduł należy zmienić znaki.. Poczytaj o wartości
bez
26 lut 21:22
Mila:
Zobacz co napisałam w punkcie (2).
Jeżeli x−1 przyjmuje wartości ujemne, to opuszczając znak |..| należy zmienić wyrażenie (x−1)
na przeciwne czyli (−x+1).
26 lut 21:26
kamczatka: A te moje wyliczenia z pierwszego posta są dobre ? Bo nie rozumiem tego rysunku wyszło −3 dla
x∊ (−∞;2) a nie przyjmuje nigdzie ten wykres wartości −3
26 lut 21:26
bezendu: Niestety są wszystkie błędne...
26 lut 21:27
kamczatka: zaraz to rozrysuje
26 lut 21:28
kamczatka:
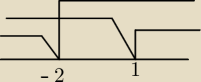
więc liczyłem to tak:
|x+2|+|1−x|
w przedziale (−
∞;−2) obie wartości są ujemne więc zmieniam znaki i wychodzi:
−x−2−1+x i wychodzi f(x)= −3
w przedziale < −2;1) pierwsza wartość jest dodatnia a druga ujemna więc zmieniam znaki tylko z
2 nawiasu:
x+2−1+x f(x)= 2x+1
W przedziale <1;
∞) obie wartości są dodatnie więc w żadnym z nawiasu nie zmieniam znaku:
x+2+1−x f(x)= 3
Gdzie ja tu błąd robię bo ciągle mi się wydaję że wszystko dobrze robię
26 lut 21:32
kamczatka: czy taki błąd robię że jak jest |1−x| to trzeba to zamienić tak aby x najpierw stał: |x−1| ?
26 lut 21:37
Mila:
Tak najlepiej jak napisałeś 21:37. Co ci napisałam w pierwszej linijce o godzinie 19:41.
Jednak jeśli masz |1−x| to badasz znak
1−x≥0 ⇔1≥x
x≤1 i w takim razie w przedziale (−∞,−2)
x+2<0 natomiast 1−x>0 a nie tak jak Ty napisałeś 21:32 w trzeciej linijce.
26 lut 21:46
kamczatka: ok dzięki
26 lut 22:25
Mila:
Cieszę się,że zrozumiałeś.

26 lut 22:29
 Dla jakiej wartości parametru p funkcja f(x) = |x + 2|+|1 − x| ma dokładnie dwa rozwiązania,
jeśli f(x) = p
Mi wychodzi tak:
dla (−∞;−2) f(x) = −3
dla < −2;1) f(x) = 2x+1
dla <1;+∞) f(x) = 3
I mi nigdzie nie wychodzi że p ma dokładnie dwa miejsca zerowe.(dodaje mój rysunek) A w
odpowiedziach mam że dla p∊ (3;∞) przyjmuje dokładnie dwa miejsca zerowe co robię źle ?
Dla jakiej wartości parametru p funkcja f(x) = |x + 2|+|1 − x| ma dokładnie dwa rozwiązania,
jeśli f(x) = p
Mi wychodzi tak:
dla (−∞;−2) f(x) = −3
dla < −2;1) f(x) = 2x+1
dla <1;+∞) f(x) = 3
I mi nigdzie nie wychodzi że p ma dokładnie dwa miejsca zerowe.(dodaje mój rysunek) A w
odpowiedziach mam że dla p∊ (3;∞) przyjmuje dokładnie dwa miejsca zerowe co robię źle ?

 |1−x|=|x−1| z definicji wartości bezwzględnej |a|=|−a|
f(x)=|x+2|+|x−1|
|x+2|=x+2 dla x≥−2
|x−1|=x−1 dla x≥1
1) x<−2
f(x)=−x−2−x+1⇔f(x)=−2x−1
2) x∊<−2,1)
f(x)=x+2−x+1⇔f(x) =3
3) x≥1
f(x)=x+2+x−1⇔f(x)=2x+1
f(x)=m ma dokładnie dwa rozwiązania dla m>3
|1−x|=|x−1| z definicji wartości bezwzględnej |a|=|−a|
f(x)=|x+2|+|x−1|
|x+2|=x+2 dla x≥−2
|x−1|=x−1 dla x≥1
1) x<−2
f(x)=−x−2−x+1⇔f(x)=−2x−1
2) x∊<−2,1)
f(x)=x+2−x+1⇔f(x) =3
3) x≥1
f(x)=x+2+x−1⇔f(x)=2x+1
f(x)=m ma dokładnie dwa rozwiązania dla m>3
 więc liczyłem to tak:
|x+2|+|1−x|
w przedziale (−∞;−2) obie wartości są ujemne więc zmieniam znaki i wychodzi:
−x−2−1+x i wychodzi f(x)= −3
w przedziale < −2;1) pierwsza wartość jest dodatnia a druga ujemna więc zmieniam znaki tylko z
2 nawiasu:
x+2−1+x f(x)= 2x+1
W przedziale <1;∞) obie wartości są dodatnie więc w żadnym z nawiasu nie zmieniam znaku:
x+2+1−x f(x)= 3
Gdzie ja tu błąd robię bo ciągle mi się wydaję że wszystko dobrze robię
więc liczyłem to tak:
|x+2|+|1−x|
w przedziale (−∞;−2) obie wartości są ujemne więc zmieniam znaki i wychodzi:
−x−2−1+x i wychodzi f(x)= −3
w przedziale < −2;1) pierwsza wartość jest dodatnia a druga ujemna więc zmieniam znaki tylko z
2 nawiasu:
x+2−1+x f(x)= 2x+1
W przedziale <1;∞) obie wartości są dodatnie więc w żadnym z nawiasu nie zmieniam znaku:
x+2+1−x f(x)= 3
Gdzie ja tu błąd robię bo ciągle mi się wydaję że wszystko dobrze robię
