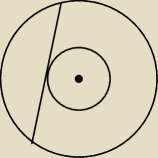
 W pierścieniu kołowym cięciwa zewnętrznego okręgu ma długość 10 i jest styczna do wewnętrznego
okręgu. Wykaż, że pole tego pierścienia można wyrazić wzorem w którym nie występują promienie
wyznaczających go okręgów.
Błagam, pomóżcie! Nie mam pojęcia od czego zacząć
W pierścieniu kołowym cięciwa zewnętrznego okręgu ma długość 10 i jest styczna do wewnętrznego
okręgu. Wykaż, że pole tego pierścienia można wyrazić wzorem w którym nie występują promienie
wyznaczających go okręgów.
Błagam, pomóżcie! Nie mam pojęcia od czego zacząć
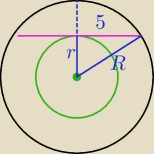 Pp=π*(R2−r2)
52+r2=R2
R2−r2=25
Dalej sama.
Pp=π*(R2−r2)
52+r2=R2
R2−r2=25
Dalej sama.
 d −− długość takiej cięciwy
d −− długość takiej cięciwy
| d | d2 | |||
R2=r2+( | )2 ⇒ R2−r2= | |||
| 2 | 4 |
| d2 | ||
P(pierścienia)= πR2−πr2=(R2−r2)*π= | *π ( nie zależy od R i r | |
| 4 |
| d | ||
d=10 , | = 5 | |
| 2 |
| d | ||
P(pierścienia)= = ( | )2*π=π*25 | |
| 2 |
