Trójkąt i ciąg arytmetyczny
mrcyvill: Witam, mam problem z poniższym zadankiem:
Długości boków trójkąta tworzą ciąg arytmetyczny. Oblicz je (długości) wiedząc, że są one
liczbami naturalnymi, a największy kąt trójkąta ma miarę 120o
Jestem w stanie policzyć z twierdzenia cosinusów (o ile nie popełniam jakiegoś błędu), że:
a1=1.5r
a2=2.5r
a3=3.5r
ale nie wiem czy dalej mogę coś z tym zrobić. A jeżeli jednak mogę, to co? Nic nie przychodzi
mi do głowy.
26 lut 17:13
PW:
a ≤ b < c
b=a+r c=a+2r
c2=a2+b2−2abcosγ
(a+2r)2 = a2 + (a+r)2 − 2a(a+r)cos120°
a2+4ar+4r2 = a2 +a2+2ar+r2 + 2a(a+r)sin30°
a2+4ar+4r2 = a2 +a2+2ar+r2 + a2 + ar
2a2 − ra − 4r2 = 0
Rachunki sprawdź!
Mamy rozwiązać równanie z niewiadomą a i parametrem r przy założeniu, że a i r są liczbami
naturalnymi − i w tym tkwi dowcip, że taki parametr jest do znalezienia (r jest naturalna i
rozwiązanie ma być liczbą naturalną).
26 lut 22:13
mrcyvill: Faktycznie, zapomniałem skreślić 2 w twierdzeniu cosinusów.
Ale czy równanie nie powinno wyglądać: 2a2 − ar − 3r2 ?
Przy takim równaniu chyba wszystkie liczby naturalne podstawione pod r dadzą poprawny wynik.
27 lut 10:13
Bogdan:
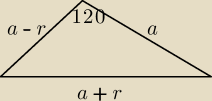
Dla uproszczenia obliczeń proponuję przyjąć oznaczenia dla ciągu arytmetycznego (a
n):
a
1 = a − r ∊ N, a
2 = a ∊ N, a
3 = a + r ∊ N
| | 1 | |
(a + r)2 = (a − r)2 + a2 + 2*a*(a − r)* |
| ⇒ ... |
| | 2 | |
27 lut 12:02
PW: Dlatego pisałem, żebyś sprawdził rachunki
2a
2 − ar − 3r
2 = 0
Δ =(−a)
2 − 4•2•(−3r
2) =25r
2;
√Δ = 5r (bo r>0).
| | r−5r | |
a = |
| nie spełnia warunków zadania |
| | 4 | |
Liczba ta jest liczbą naturalną wtedy i tylko wtedy, gdy r jest liczbą parzystą.
Tak więc dla r=2k, k∊N mamy trójkąt o bokach
a=3k, b = b=3k+2k = 5k, c = 5k+2k = 7k
Odpowiedź: Warunki zadania spełnia trójkąt o bokach 3, 5, 7 i każdy podobny do niego, jeżeli
skala podobieństwa jest liczbą naturalną.
Twoje rozwiązanie z 26 lutego o 17:13
było więc dobre − wystarczyło zauważyć, że skoro
długości boków mają być liczbami naturalnymi, to r musi być parzysta.
27 lut 15:24
mrcyvill: Dzięki. Bardzo mi pomogliście. Niby takie proste zadanie, a sprawiło mi nie lada problem.
Chyba muszę wziąć się ostro za arkusze, żeby nie wylądować w takiej sytuacji na maturze

Jeszcze raz wielkie dzięki.
28 lut 00:27
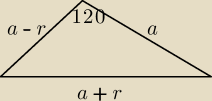 Dla uproszczenia obliczeń proponuję przyjąć oznaczenia dla ciągu arytmetycznego (an):
a1 = a − r ∊ N, a2 = a ∊ N, a3 = a + r ∊ N
Dla uproszczenia obliczeń proponuję przyjąć oznaczenia dla ciągu arytmetycznego (an):
a1 = a − r ∊ N, a2 = a ∊ N, a3 = a + r ∊ N
 Jeszcze raz wielkie dzięki.
Jeszcze raz wielkie dzięki.