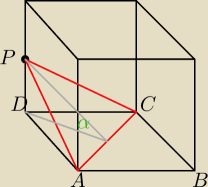
Stereometria ReVo: Sześcian o krawędzi a przecięto płaszczyzną przechodzącą przez przekątną dolnej podstawy i punkt P leżący na krawędzi bocznej rozłącznej z tą przekątną. Otrzymany przekrój jest

	2
trójkątem nachylonym do płaszczyzny podstawy pod kątem, którego sinus jest równy		.
	3

Wyznasz odległość punktu P od dolnej podstawy sześcianu i pole przekroju'.

ReVo: Ktoś podpie jak w ogóle zacząć? |E− srodek AC

	a * √2
|AE| =
	2

	|PD|		2
sin α =		=
	|PE|		3

ReVo: Rysunek może być błędny bo to ja to tak zrozumiałem...

Mila: Oblicz cosα ( jedynka tryg.), potem tg α , α− kąt ostry. Dalej powinieneś sobie poradzić.

ReVo:

	2√5
Obliczyłem tgα =
	5

	|PE|		2√5
tgα =		=		i nie wiem co dalej
	DE		5