Podstawą ostrosłupa jest Matejko: Podstawą ostrosłupa jest prostokąt o bokach 4 i 4√2 wszystkie krawędzie boczne ostrosłupa mają długość 4. Oblicz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa. to jest ten rysunek? a=4 b=4√2 liczymy ten kąt zaznaczony na rysunku? liczymy wysokość trójkąta o podtsawie a i o podtawie b i przekątna tak?

Matejko:

Matejko: up

Ajtek: https://matematykaszkolna.pl/forum/239172.html Ile razy można?

Matejko: pytam bo nie wychodzi i jak w podstawie jest prostokąt to jest inny kąt chyba.

Matejko: http://forum.zadania.info/viewtopic.php?f=21&t=33112 tu jest podany inny kąt i im wychodzi a ja tego nie rozumiem, dlatego pytam..

Ajtek: Faktycznie, to nie jest ten kąt .

Matejko: mógłby ktoś rozwiązać to zadania? Proszę

Matejko: up

Mila: Tu jest pułapka w tym zadaniu, jaki wynik podają? Dwie ściany boczne są Δ prostokątnymi, a dwie Δ równobocznymi.

Matejko:

	√3
wynik to −		proszę o dokładne rozpisanie i wyjaśnienie
	3

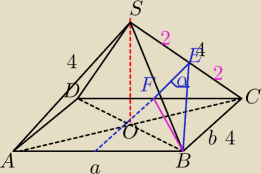
Mila: a=4√2 ΔBCS≡ΔADS − Δ równoboczne. ΔABS≡ΔDCS− Δ prostokątne równoramienne, bo z tw. odwrotnego do tw. Pitagorasa. a²=4²+4² a²=32 a=4√2⇔DS⊥CS BE⊥SC, z punktu E prowadzimy równoległą do DS, w takim razie jest prostopadła do ramienia SC. Z tw. Talesa wyciągamy wniosek, że F jest w środku DC. |FE|=2

	4√3
|BE|=
	2

|BE|=2√3 jako wysokość Δ równobocznego o boku 4. W ΔFCB: |FB|²=(2√2)²+4² |FB|²=24 W ΔFEB z tw. cosinusów: |FB|²=|FE|²+|BE|²−2*|FE|*|BE|*cosα 24=2²+(2√3)²−2*2*2√3 cosα⇔

	−1
cosα=
	√3

	√3
cosα=−
	3

Matejko: nie rozumiem jak było FB liczone

Mila: Z tw. Pitagorasa. |FC|=2√2 − połowa boku a |BC|=4 ∡FCB=90^o

Matejko: a no tak dzięki

Mila: