różne, różniste..... Saizou : Witam Was wszystkich macie czas na jakieś zadanka spod gwiazdy "matura w maju" tak mi się nudzi więc pomyślałem że 30 min poświęcę na szlify matematyki

Godzio:

Marcin: Bierz się za polski, matmę ogarniasz Siema

Eta:

Saizou : haha trzeba by bibliografię skończyć ale to w piątek a teraz coś przyjemniejszego

Godzio: Dany jest wierzchołek kwadratu A(1,−3) i równanie prostej y = 2x, w której zawiera się jedna z przekątnych tego kwadratu. Wyznacz współrzędne pozostałych wierzchołków tego kwadratu. (zadanie z matury 1975)

bezendu: Godzio to zadanie raczej z podstawy niż z R

Hajtowy: No to dawaj! 3 zadanka na rozgrzewkę. Zadanie 1 Obecnie 1kg cukru kosztuje o 3,20 zł więcej niż kilka lat temu. Wówczas za kwotę równą 225 zł można było kupić o 80 kg więcej cukru niż obecnie. Ile kosztuje 1 kg cukru obecnie? Zadanie 2 Prostokątny pas wykładziny dywanowej o wymiarach 3,6m na 7,5m należy przeciąć prostopadle do dłuższego boku tak, aby przekątne otrzymanych dwóch prostokątnych kawałków różniły się o 1,5m. Oblicz wymiary większego z otrzymanych kawałków. Zadanie 3 Ze zbioru wszystkich liczb naturalnych czterocyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia, że otrzymamy liczbę spełniającą jednocześnie trzy następujące warunki: (1) liczba jest podzielna przez 25 (2) cyfry dziesiątek i setek są nieparzyste (3) cyfra dziesiątek jest nie większa niż cyfra setek

Saizou : Szukane punkty to (0:0), (−3:−1), (−2:−4)

Saizou : a może coś z rozszerzenie

Trivial: Udowodnij twierdzenie Pitagorasa.

ZKS: Rozłóż wielomian na czynniki W(x) = x⁴ + x³ + x² + x + 1.

ICSP: Znajdź takie wartości parametru m dla których równanie : sin(3x) = msin(x) ma rozwiązanie.

Trivial: ICSP, tamto zadanko z układem w liczbach całkowitych jest nierozwiązywalne... Sprawdziłem, że w przedziale |d| ≤ 10000 rozwiązanie jest tylko dla d = −1.

ICSP: Zobaczymy co Vax powie

Norfolk: sin(3x)=msin(x) Czy powinno byc m∊[−1,3]?

Mila: (−2,1,1,−1) (1,−2,1,−1) (1,1−2,−1)

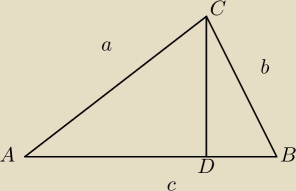
Saizou : tw. Pitagorasa np. ΔABC~ΔBCD~ΔACD (kk)

a		AD
	=
c		a

a²=clADl

b		DB
	=
c		b

b²=clBDl a²+b²=c(AD+BD)=c²

Wazyl: dla sinx=0 równanie zawsze ma rozwiązanie, prawda?

ICSP: Dla kogo w końcu są te zadania ...

Norfolk: Zawsze nie. Ale rozwiazanie ma.

Eta: Dla maturzystów

Kamix: Vax juz odpowiedzial wam na tamto zadanie

ZKS: Norfolk o ile się nie pomyliłem to Twoja odpowiedź ale niech ICSP powie czy na pewno.

ICSP: pytałem o wartości m

Wazyl: Niezależnie od m równanie zawsze ma rozwiązanie o ile się nie mylę. x=0

ICSP: to nadal nie jest podana odpowiedź

Norfolk: Czyli m∊[−1,3] to zla odpowiedz?

ICSP: zła

Wazyl: ICSP przepraszam że się włączę/yłem czy x∊R jest poprawną odp?

Saizou : 3sinx−4sin³x=msinx sinx(3−m−4sin²x)=0

	3−m		3−m
sinx=0 lub sin2x=		sin2x∊<0:1>⇒0≤		≤1⇒m∊<−1:3>
	4		4

ICSP: nie. x ∊ R nie jest poprawną odpowiedzią.

Norfolk: No ja robilem dokladnie jak Saizou...

ZKS: Nie spojrzałem dokładnie na polecenie jaki dał ICSP. Dałem sam się złapać. Wazyl przecież pytają o m nie o x.

Wazyl: ZKS gafa. m∊R

ZKS: To przeczytaj polecenie sobie jeszcze raz a zrozumiesz o co chodzi.

ZKS: Mój post był do Norfolk.

ICSP: m ∊ R to poprawna odpowiedź

Saizou : m∊<−1:1>

Norfolk: Niezaleznie od m ze wzgledu na to, ze mamy tam alternatywe i w jej sklad wchodzi sinx=0, tak?

Jolanta: Mógłby ktoś zerknac na moje zadanie ?

Saizou : ech... mykam spać bo nie myślę, jedyne co do wielomianu to wymyśliłem że jest to równoznaczne z

	x5−1
zapisem
	x−1

ZKS: Haczyk był fajny ICSP już mi na mózg coś poszło że od razu nie zauważyłem co dokładnie chce polecenie. To Saizou masz jeszcze zadanie te które podał Trivial i ja.

ZKS: Chcesz podpowiedź do tego wielomianu?

Trivial: Moje już chyba rozwiązał.

Saizou : na razie nie, a pitagorasa udowodniłem

ZKS: Racja przepraszam. To chyba rzeczywiście czas na mnie.

Norfolk: Jak rozumiem ten haczyk byl wlasnie w tej alternatywie? Dla sinx=0 znajdziemy rozw., wiec nawet

	3−m
jestli sin2x=		jest sprzeczne, to to nic nie zmienia, tak? Zadanko rzeczywiscie
	4

genialne.

Domel: A może coś z rocznika '80 W trójkącie prostokątnym wysokość poprowadzona z wierzchołka kąta prostego ma długość 1 i dzieli ona przeciwprostokątną na dwie części. Oznaczając długość jednej z tych części przez "x" a długość przeciwprostokątnej przez "y" wyznaczyć y jako funkcję x oraz obliczyć jej najmniejszą wartość.

Domel: Udowodnić, że trapez o podstawach AB i CD ( |AB| > |CD| ) można podzielić prostą równoległą do któregokolwiek boku nie będącego podstawą na dwa czworokąty o równych polach wtedy i tylko wtedy gdy |AB| < 3|CD|

Domel: a przy zadaniu z sinusami nie można zapisać?

	4
x∊R => m∊<−1; 3> ∧ m = −		sin2x
	3

nie bardzo rozumiem ostatni tekst Norfolka

Norfolk : W zadaniu szukamy m takiego, ze sin(3x)=msinx ma rozwiazanie. Dochodzimy do postaci sinx(3 − m − 4sin²x)=0, czyli

	3 − m
sinx = 0 lub sin2x =
	4

Dla sinx = 0 zawsze znajdziemy jakies rozwiazanie. Wezmy przykladowo m = 15. Wtedy mamy:

	−12
sin2x =		, sin2x = −3. Oczywiscie wtedy rownanie jest sprzeczne, ale mamy i tak:
	4

sinx = 0 lub sin²x = −3. Zauwaz, ze dla tego m = 15 ta alternatywa dalej ma rozwiazanie [bo oczywiscie sinx = 0 ma rozwiazanie], wiec cale rownanie − sin(3x)=msinx ma rozw. Uogolniajac, dla m∊R rownanie dalej ma rozwiazanie, stad takie rozwiazanie.

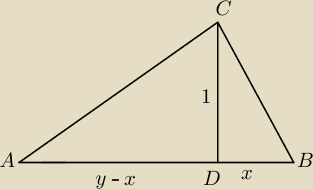
Saizou : W trójkącie prostokątnym wysokość poprowadzona z wierzchołka kąta prostego ma długość 1 i dzieli ona przeciwprostokątną na dwie części. Oznaczając długość jednej z tych części przez "x" a długość przeciwprostokątnej przez "y" wyznaczyć y jako funkcję x oraz obliczyć jej najmniejszą wartość. ΔACD~ΔBCD (kk)

1		y−x
	=
x		1

	x2+1
y=		i 0<x<y
	x

korzystając z nierówności o średnich

	x2+1
√		≥√x
	2

x2+1
	≥2
x

	x2+1
zatem najmniejsza wartość jaką przyjmuje funkcja		dla 0<x<y to 2
	x

o to chodzi ?

Eta: Dokładnie o to

Saizou : a z dziedziną wszystko ok ?

Saizou : Udowodnić, że trapez o podstawach AB i CD ( |AB| > |CD| ) można podzielić prostą równoległą do któregokolwiek boku nie będącego podstawą na dwa czworokąty o równych polach wtedy i tylko wtedy gdy |AB| < 3|CD| a tutaj co będzie tezą do udowodnienia, jak nigdy nie mam problemów z tym to tutaj mam xd

ZKS: Jak tam wielomian ruszył coś czy nie bardzo?

Saizou : niestety nie, ale myślę że to będzie się wiązać z jakimś dzieleniem obustronnym

Saizou : znaczy się ja rozpatruję x⁴+x³+x²+x+1=0

ICSP: Przedstawiłem już na forum chyba ze 3 razy sposób rozwiązywania takich równań xD

Saizou : to najwyraźniej ich nie widziałem, albo nie pamiętam

ZKS: Jeżeli Ci łatwiej to i możesz jako równanie Twój cyrk Twoje małpki.

ZKS: A przez co byś dzielił to równanie?

ICSP: No to teraz Saizou sam opracujesz metodę rozwiązywania równania w postaci : a⁴ + bx³ + cx² + bx + a = 0

ZKS: "ax⁴ + ..."

Saizou : sam jeszcze nie wiem

ZKS: Jeżeli to będzie wskazówka to powiem że to dobry trop podzielenie przez coś.

ICSP: ale najpierw trzeba coś założyć Nie chcemy przecież dzielić przez 0

ZKS: To już masz dwie wskazówki.

Saizou : chyba już wiem x⁴+x³+x²+x+1=0 /: x² dla x≠0, gdyby x=0 mamy sprzeczność

	1		1
x2+		+x+		+1=0
	x2		x

	1		1		1
(x+		)2+x+		−1=0 x+		=t
	x		x		x

t²+t−1=0 Δ=1+4=5 √Δ=√5

	−1−√5		−1+√5
t1=		t2=
	2		2

	1+√5		1−√5
(t+		)(t+		)=
	2		2

	1		1+√5		1		1−√5
(x+		+		)(x+		+		)
	x		2		x		2

ICSP: to teraz jeszcze zrób z tego wielomian. I pokaż, ze ten rozkład działa również dla x = 0

Saizou :

	1		−1−√5
x+		=
	x		2

2x²+2=(−1−√5)x 2x²+(1+√5)x+2=0 analogicznie dla

	1		−1+√5
x+		=
	x		2

2x²+(1−√5)x+2=0 (2x²+(1+√5)x+2)(2x²+(1−√5)x+2)

ICSP: żle

Saizou : a to czemu?

Trivial: Saizou, przy próbie wymnożenia, nie ma zgodności już dla x⁴. Coś źle.

ICSP: Czy : wielomian wyjściowy = wielomianowi końcowemu ?

ICSP: o_o Witaj Trivial

Saizou : już chyba wiem

1
	(2x2+(1+√5)x+2)(2x2+(1−√5)x+2)
4

ale czemu tak to nie wiem xd

Saizou : a.... bo mnożyłem /*2 i to zwiększyło współczynniki,i trzeba je zniwelować

Trivial: O_o Witaj ICSP

ICSP: To teraz zajmij się przypadkiem ogólnym

Saizou : ja się żegnam teraz bo jutro szkoła, tak wiec dzięki za pomoc wszystkim xd i dobranoc

Trivial: ICSP, ale Cię Saizou załatwił.

ICSP: nie wymiga się od tego Potem będzie rozważał przypadek dla równania zwrotnego stopnia VI

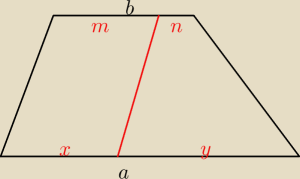
Domel: No i jak myślisz − kiedy ta czerwona kreska podzieli czarny trapez na dwa czworokąty a kiedy to będzie np. czworokąt i trójkąt albo pięciokąt i trójkąt? I pamiętaj, że nas interesują dwa czworokąty o tych samych polach

Domel: A w trójkącie gdybyś zapomniał o nierówności średnich to możesz zastosować pochodną funkcji (na maturze rozszerzonej chyba jest pochodna − a właśnie pochodna = 0 pokazuje nam miejsce ekstremum czyli minimum lub maximum funkcji). Jak masz ochotę to możesz też poćwiczyć ten sposób.

Saizou: Domel, jestem niesczesliwym rocznikiem z 95, ktory nie mial pochodnych, granic i wielu innych ciekawych rzeczy, ale jakos sobie trzeba dawac rade wiec bardzo przepraszam i nie policze pochodnej

Domel: wszystko przed tobą − bo widzę, że z takim zaangażowaniem to się chyba na szkole średniej nie skończy. A swoją drogą mam nadzieję, że na polaka i obcy pozostało ci choć 20% czasu

Saizou : Domel ale co będzie tezą? To że odcinek czerwony dzieli trapez na 2 czworokąty o równych polach, czy |AB| < 3|CD|

Domel: A może popatrzysz w ten sposób: Żeby uzyskać po podziale 2 czworokąty to hmmmm...... n jest hmmm......... (no bo chyba jest?) A potem − masz proporcje powierzchni nowych czworokątów względem siebie i względem trapezu

Domel: Inaczej − jakie jest to n

Saizou : Domel nie chodzi mi o sposób rozwiązania tylko o formalny zapis

zawodus : Wiedzę, że się nudzisz może zadanko?

Domel: Założenie: Żeby były 2 czworokąty to Teza n>0

DobryGees: Matematyka to zuo ;<

Domel: I dla DobrychGeesów polski też

Saizou : szczerze mówiąc jeszcze pomyślę bo nie miałem zbytnio czasu xd

Domel: Wylicz n, skorzystaj z tezy i wcześniejszych podpowiedzi a doznasz objawienia

Saizou :

	1
mh=		(n+y)h
	2

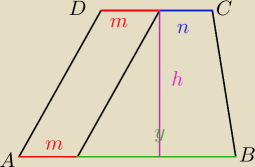
2m=n+y n=2m−y wiemy że n>0 2m−y>0 2m>y /+m 3m>m+y 3m>lABl a dalej..... <myśli>

domel: A może zamiast przyrównywać 2 małe czworokąty to porównać czworokąt z połową trapezu?

domel: 1. Oblicz m (bez zależności od n) 2. Oblicz n 3. Wykorzystaj warunek na n

ahhh ta matematyka: ale z Was mózgi

pigor: ..., a mnie się spodobało zad.1 z dnia 25.02 22 : 40 Obecnie 1kg cukru kosztuje o 3,20 zł więcej niż kilka lat temu. Wówczas za kwotę równą 225 zł można było kupić o 80 kg więcej cukru niż obecnie. Ile kosztuje 1 kg cukru obecnie ? −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− ..., np. tak: równaniem , gdzie x=? − szukana cena 1kg cukru :

225		225
	=		+ 80 /* 15 x(x−3,2) ix >3,2 ⇔
x−3,2		x

⇔ 45x= 45(x−3,2)+16x(x−3,2) ⇔ 16x(x−3,2)= 45*3,2 /: 16 ⇔ ⇔ x(x−3,2)= 9 ⇒ x(x−3,2)= 5*1,8= 5*(5−3,2) ⇒ x=5 [zł] .