zrobilem sobie rysunki tych figur tylko nie wiem jak to ze soba powiazac Zero:  Wyznacz i porównaj pola powierzchni brył obrotowych otrzymanych przez obrót sześciokąta foremnego o boku a dookoła następujących osi: a) prostej przechodzącej przez środki przeciwległych boków sześciokąta, b) prostej zawierającej dłuższą przekątną sześciokąta, c) prostej zawierającej bok sześciokąta.

dero2005:

dero2005:

dero2005:

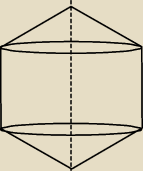
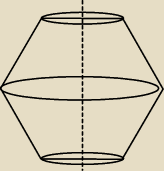
Zero: Dokladnie. Figure na obrazku nr. 2 obliczylem. Prπobowalem ta pietwsza ale wychodzi mi zla liczba. Są tam dwa jednakowo obciente stozki. Z talesa obliczylem ze l tej brakujacej czesci jest rowne A. Dalej zas chcialem zapisac rownaniem: Pb = 2( πa*2a − π ¹₂a*a) gdzie pierwsza czesc to pb duzego stozka drugi wzor to pb mniejszego ktorego przeba odjąc

dero2005: Fig 1 P_b = πl(R+r) pow boczna jednego stożka ściętego gdzie l = a R = a

	a
r =
	2

dero2005: dodać pow dna i wieka 2πr²

Zero: Wlasnie, zapomnialem o tych dwoh kolach na gorze i dole xD

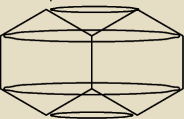
dero2005: Fig 3 pow boczna walca P_w = 2πrh gdzie : r = a√3, h = a plus powierzchnia boczna dwóch stożków ściętych

	a√3
2*Pb = 2*πl(R+r) gdzie: l = a , R = a√3, r =
	2

plus powierzchnia boczna dwóch stożków

	a√3
2*Pb = 2*πrl gdzie: l = a, r =
	2